Totes les lletres de la paraula $\boxed{\text{VOTO}}$ tenen un eix de simetria vertical i per tant aquesta és la solució.

El perímetre del triangle és $6+10+11=27$. Un triangle equilàter té els tres costats de la mateixa longitud, i per tant el costat és:

$$c=\frac{27}3=\boxed{9}$$

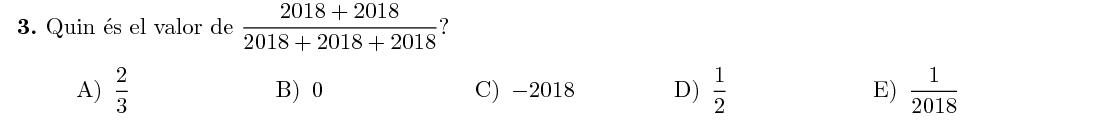
Simplifiquem la fracció:

$$\frac{2018+2018}{2018+2018+2018}=\frac{2\cdot2018}{3\cdot2018}=\boxed{\frac23}$$

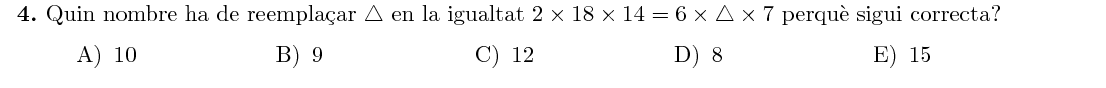
Podem aïllar el triangle i simplificar fàcilment:

$$\triangle=\frac{2\times18\times14}{6\times7}=2\times\frac{18}6\times\frac{14}7=2\times3\times2=\boxed{12}$$

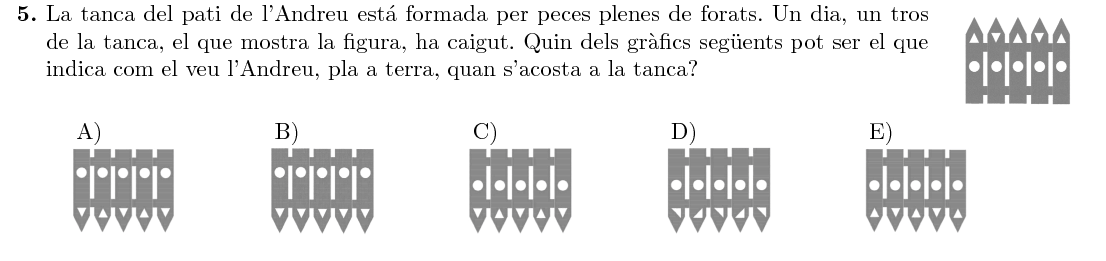
Podem descartar els dibuixos $A$ i $B$ perquè tenen els cercles massa a prop de la base de la tanca.

Pel que fa a la resta, l'opció $\boxed{\text{C}}$ és l'única que té els triangles ben orientats.

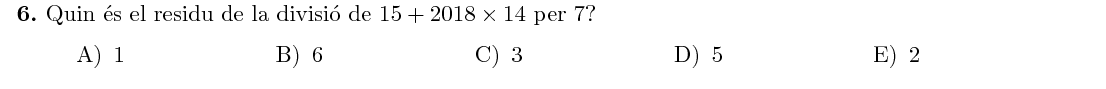
Com que $2018\times14$ és múltiple de $7$, el residu d'aquest sumand és zero.

Per tant, el residu de la suma serà el residu de dividir $15$ per $7$, que és $\boxed1$.

En el pitjor dels casos, hi haurà un terç de persones a qui no agrada el futbol, però sí el tennis.

Per tant, dels $\frac34$ aficionats del tennis, també els agrada el futbol a: $$\frac34-\frac13=\frac9{12}-\frac4{12}=\boxed{\frac5{12}}$$

Hi ha $\boxed{4}$ camins possibles:

Per la figura sabem que $5$ costats curts es corresponen amb $2$ costats llargs. Per tant, el costat curt mesura:

$$\text{costat curt}=\frac25\cdot10=4$$

El perímetre del rectangle gran està format per $6$ costats llargs i $4$ de curts, és a dir:

$$\text{P}=6\cdot10+4\cdot4=\boxed{76}$$

Els cercles tenen diàmetre $7$, i per tant, radi $3.5$.

Cadascun dels centres està a $3.5$ dels extrems dret i esquerre del rectangle, i per tant estan a una distància entre ells de:

$$d=11-3.5-3.5=\boxed{4}$$

El quadrat té àrea $3\times3=9$, i el triangle $\triangle DMC$ té una àrea que és un terç d'aquesta àrea, és a dir, $3$.

Com l'altura del triangle $\triangle DMC$ és $3$, amb la base $DM$, la fórmula de la seua àrea és:

$$A_{\triangle DMC}=\frac12\times \overline{DM}\times3=3$$

I si aïllem $\overline{DM}$ tenim:

$$\overline{DM}=\boxed2$$

Provant una mica és fàcil adonar-se que la multiplicació ha de ser:

$$13\times24=312$$

Per tant la suma dels tres dígits és:

$$S=1+4+1=\boxed6$$

En primer lloc, intentem esbrinar la mida del rectangle. Anomenem $a,b$ els dos costats del rectangle (el nombre de files i columnes de quadradets).

Sabem que $a\times b=40$, i que $a,b>1$. Per poder parlar d'una fila del mig, cal que $a$ sigui senar, i per tant $b$ ha de ser parell.

La descomposició en factors primers de $40$ és $40=2^3\cdot5$. Per tant, necessàriament el nombre de files i columnes serà: $a=5, b=8$.

La fila del mig té $8$ quadrats, i sense pintar en queden $40-8=\boxed{32}$.

Si el regal fos a la caixa $1$, llavors les dues primeres pistes serien certes, cosa que no pot ser.

Si el regal fos a la caixa $2$, cap de les tres pistes seria certa, però sabem que una ho ha de ser.

Per tant, el regal és a la caixa $\boxed3$.

Començant per dalt, i partint d'una recta horitzontal, realitzem un gir negatiu de $-10^\circ$ i després un positiu de $14^\circ$, obtenint una recta amb $4^\circ$ positius.

Per baix, l'operació que hem de fer és $26-33=-7^\circ$.

Entre ambdues rectes formen un angle de:

$$\alpha=4-(-7)=\boxed{11^\circ}$$

Anomenem $x,y$ els dos primers nombres de la seqüència:

$$x\quad y\quad 1\quad\text{\textunderscore}\quad\text{\textunderscore}\quad\text{\textunderscore}\quad\text{\textunderscore}\quad32$$

Si emplenem els buits amb el producte dels dos nombres anteriors tenim:

$$x\quad y\quad (x\cdot y=1)\quad y\quad y\quad y^2\quad y^3\quad (y^5=32)$$

Però resulta que $32=2^5$, i per tant $y=2$. Llavors:

$$x\cdot y=1 \quad\Rightarrow\quad 2x=1 \quad\Rightarrow\quad x=\boxed{\frac12}$$

L'any $2018$ té $365$ dies, per tant aquesta illa tindrà 15 dies núvol.

En el pitjor dels casos, el primer dia de la Carla a l'hotel farà sol, però el dia següent estarà núvol, cosa que es repetirà durant $30$ dies en total.

Llavors, necessàriament tindrà dos dies de sol seguits. En total, haurà hagut d'esperar $\boxed{32}$ dies.

Si la Carme ha gastat $c$, llavors la Berta ha gastat $0.15c$ i l'Àlia $1.6c$. En total, les tres han gastat:

$$1.6c+0.15c+c=2.75c=55$$

Podem aïllar la $c$ i esbrinem que la Carme va gastar:

$$c=\frac{55}{2.75}=20$$

Per tant, Àlia va gastar:

$$a=1.6c=\boxed{32}$$

L'àrea d'un triangle és la meitat de la base per l'altura. En el nostre cas, els dos triangles tenen la mateixa base (el costat llarg del rectangle). A més, les sumes de les seves altures és també l'altura del rectangle.

En conclusió, la suma de les àrees dels dos triangles és la meitat de l'àrea del rectangle, és a dir, $\boxed{20\text{ cm}^2}$.

Si sumem les tres files i les tres columnes, sumem cada nombre dos cops. En total, sumarem:

$$S=2\cdot(1+2+\cdots+8+9)=2\cdot45=90$$

La suma dels cinc resultats que sabem són:

$$12+13+15+16+17=73$$

I per tant el sisè resultat serà: $90-73=\boxed{17}$.

Anomenem $x_1,x_2,\ldots,x_{11}$ els punts, ordenats d'esquerra a dreta. Llavors, les sumes són:

$$2018=(x_2-x_1)+(x_3-x_1)+\cdots+(x_{11}-x_1)=-10x_1+(x_2+x_3+\cdots+x_{11})$$ $$2000=(x_2-x_1)+(x_3-x_2)+\cdots+(x_{11}-x_2)=-x_1-9x_2+(x_2+x_3+\cdots+x_{11})$$

Si restem les dues equacions, obtenim:

$$18=-9x_1+9x_2=9(x_2-x_1)$$

I per tant, la distància entre els dos primers punts és:

$$x_2-x_1=\frac{18}{9}=\boxed2$$

Anomenem $a,b,c$ els tres costats, tal com es mostra a la figura:

Llavors les tres mesures del dibuix es corresponen a les següents equacions:

$$ \begin{cases} a+c=10 \\ b+c=7 \\ 2a+2b=26 \\ \end{cases} $$

Restant les dues primeres equacions deduim que:

$$a-b=3\quad\Rightarrow\quad a = 3+b$$

Substituint a la tercera equació trobem $b$:

$$2a+2b=6+2b+2b=6+4b=26\quad\Rightarrow\quad 4b=20\quad\Rightarrow\quad b=5$$

Per tant:

$$a=3+b=3+5=8$$

I finalment:

$$a+c=10\quad\Rightarrow\quad8+c=10\quad\Rightarrow\quad c=2$$

Hem trobat que els tres costats mesuren $2,5,8$. Llavors, el volum és:

$$V=2\times5\times8=\boxed{80\text{ cm}^3}$$

Considerem $4$ nombres consecutius qualsevols en aquest requadre: $a,b,c,d$. Com cada nombre és la suma dels dos que són a la vora, resulta que:

$$b = a + c$$ $$c = b + d$$

Si aïllem $c$ a la primera equació, tenim que $c=b-a$, i substituint a la segona:

$$b-a=b+d \quad\Rightarrow\quad -a=d$$

El que hem deduit, és que cada $3$ elements en aquesta seqüència, obtenim el nombre original amb el signe canviat. Si anem omplint a partir del $10$ i el $3$, obtenim:

I per tant, $x=-3+10=\boxed7$

La Isabel ha fet $6$ llargs de piscina, és a dir, $300\text{ m}$. Com en Simó corre $3$ cops més ràpid, en el mateix temps ha corregut $900\text{ m}$. Com sabem que ha fet $5$ voltes, una volta a la piscina mesura: $\frac{900}5=180\text{ m}$. Finalment, una volta a la piscina és la suma dels $4$ costats. Si anomenem $c$ el costat que no coneixem:

$$180=2\times50 + 2\times c\quad\Rightarrow\quad c=\frac{180-100}2=\boxed{40}$$

Dels $130$ vots, queden per comptar:

$$\text{queden}=130-(24+29+37)=40$$

En el pitjor dels casos, en Biel rebria $8$ vots més, i llavors estarien empatats a $37$ i quedarien $32$ vots per comptar.

Per tant, la Carla necessitaria més de la meitat d'aquests $32$ vots, és a dir, un total de $\boxed{17}$.

En primer lloc, comprovem que l'àrea del colom és exactament la meitat de la bandera. Ho podem fer trobant les següents equivalències (iguals colors són iguals àrees):

Per tant, l'àrea de la bandera és:

$$A_\text{bandera}=192\times2=384$$

Sabem que la proporció de la bandera és $6$ a $4$, i per tant les mides $a,b$ compleixen:

$$\begin{cases} ab=384\\ 6a=4b \end{cases}$$

Resolem el sistema:

$$a=\frac46b\quad\Rightarrow\quad \frac46b^2=384\quad\Rightarrow\quad b^2=576\quad\Rightarrow\quad b=24\quad\Rightarrow\quad a=16$$

I per tant la bandera mesura $\boxed{24\text{ cm}\times16\text{ cm}}$.

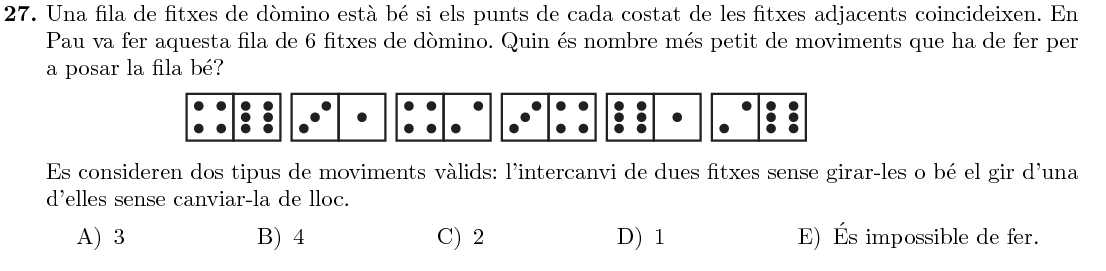
Fixem-nos que inicialment, cap de les $5$ parelles de nombres coincideixen.

Observem que els dos $3$ que tenim apareixen a la banda esquerra de les peces, i per tant li haurem de donar la volta a una de les dues peces que tenen un $3$. Aprofitant que els dos $1$ que tenim apareixen a la dreta, sembla que el més adient serà girar la peça $31$.

Però llavors cap de les $5$ parelles de nombres adjacents coincideixen. En substituir una peça per una altra, podem com a molt canviar $4$ adjacències, i per tant necessitarem dos moviments com a mínim.

Amb $3$ moviments en total, hem trobat la següent seqüència:

Podem dividir l'hexàgon en $6$ triangles equilàters formats pel centre i cadascun dels costats. Aquests triangles tenen un costat que és $\frac{DE}2$, i una àrea de $\frac16$.

Per tant, el triangle gran, que té un costat que és $3DE$, té un costat $6$ vegades més llarg que el dels triangles petits. Com ambdós són triangles equilàters, i per tant semblants, l'àrea del gran serà $6^2=36$ vegades major, és a dir:

$$A=36\cdot \frac16=\boxed6$$

Suposem que ha fet $n$ salts quan porta una mitjana de $3.80$. Després de saltar $3.99$, la mitjana ha augmentat en $1$ cm:

$$3.81=\frac{3.80n+3.99}{n+1}\quad\Rightarrow\quad 3.81n+3.81=3.80n+3.99\quad\Rightarrow$$ $$\Rightarrow\quad 0.01n=0.18 \quad\Rightarrow\quad n=18$$

Per tal que la mitjana augmenti un altre centímetre, necessitem que:

$$3.82=\frac{3.81\cdot19+x}{20}\quad\Rightarrow\quad 3.82\cdot20=3.81\cdot19+x\quad\Rightarrow$$ $$\Rightarrow\quad 76.40 = 72.39 \quad\Rightarrow\quad x=4.01$$

Així, el pròxim salt ha de ser de $\boxed{4.01\text{ m}}$.

En primer lloc, observem que com el triangle $\triangle MNP$ és isòsceles, els costats $MN$ i $NP$ són iguals, i per tant $LP=KN=MP$:

Anomenem $\alpha$ l'angle que volem esbrinar i anomenem la resta d'angles amb diverses lletres gregues:

Ara anirem resolent poc a poc el valor de cadascun d'aquests angles.

Com els tres angles d'un triangle sumen $180^\circ$, tenim que:

$$\alpha+\alpha+\beta=180 \quad\Rightarrow\quad \beta=180-2\alpha$$

D'altra banda, $\delta$ és el suplementari de $\alpha$:

$$\delta = 180-\alpha$$

Els tres angles de $\triangle MKL$ també sumen $180^\circ$:

$$\delta+2\gamma=180\quad\Rightarrow\quad \gamma = \frac{180-\delta}2=\frac{180-(180-\alpha)}2=\frac\alpha2$$

I també sabem que els tres angles $\beta,\gamma,\varepsilon$ sumen $180^\circ$:

$$\beta+\gamma+\varepsilon=(180-2\alpha) +\frac\alpha2 + \varepsilon = 180 \quad\Rightarrow\quad \varepsilon=\frac32\alpha $$

Finalment, com $\triangle MNP$ és isòsceles, sabem que:

$$\zeta = \varepsilon + \gamma = \frac32\alpha + \frac\alpha2 = 2\alpha$$

Hem esbrinat, per tant, que el triangle té els següents angles:

I com tots tres han de sumar $180^\circ$, $\alpha$ mesura:

$$5\alpha=180\quad\Rightarrow\quad \alpha=\boxed{36^\circ}$$