Solucions del Cangur 2017 a Catalunya: 4t d'ESO
Descobreix la Contrarellotge matemàtica, el portal de concursos matemàtics online.
Ací teniu el recull de solucions del Nivell de 4t d'ESO del Cangur de Catalunya de 2017. Els enunciats estan extrets del primer model d'examen del pdf d'enunciats. Les solucions estan amagades (cal fer clic per mostrar-les) perquè és recomanable pensar detingudament cada problema abans de mirar la solució que jo proposo!
Podeu accedir a les qüestions directament:
- Qüestions de 3 punts: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10.
- Qüestions de 4 punts: 11, 12, 13, 14, 15, 16, 17, 18, 19, 20.
- Qüestions de 5 punts: 21, 22, 23, 24, 25, 26, 27, 28, 29, 30.
Els enunciats del Cangur són propietat de la Societat Catalana de Matemàtiques i Le Kangourou sans Frontières.
Qüestions de 3 punts
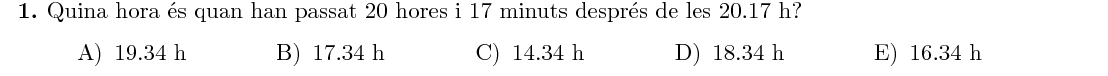
Després de $17$ minuts, són les $20.34$. Després de $4$ hores són les $00.34$, i $16$ hores després, finalment, són les $16.34\text{ h}$.

Entre Núria i Maria hi ha $3$ noies per una banda i $6$ per l'altra. En total, són: $$ N=3+6+1+1=11 $$
 Mostra solució ▾
Mostra solució ▾Si canviem l'orientació dels segments, podem construir un triangle equilàter gran amb la línia discontínua com a base. Llavors, la línia negra seran els altres dos costats del triangle equilàter. Com la base mesura $200\text{ m}$, el camí negre mesurarà $2\cdot200=400\text{ m}$.

Expressem l'enunciat amb una equació, en què $x$ és la capacitat del dipòsit, i la resolem: $$ 0.75x = 0.25x+25\quad\Rightarrow\quad 0.5x=25\quad\Rightarrow\quad x=50 $$
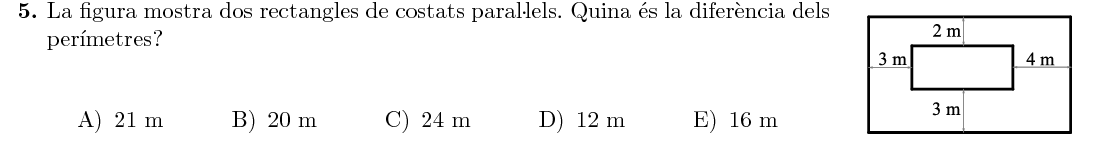 Mostra solució ▾
Mostra solució ▾Tenim les mesures de la diferència entre costats, i la diferència dels perímetres és el doble de la suma d'aquestes diferències: $$ D=2\cdot(3+2+4+3)=24\text{ m} $$
 Mostra solució ▾
Mostra solució ▾Podem dividir la figura en petits triangles equilàters iguals:
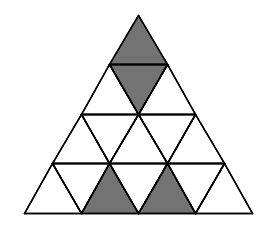
La part que està ocupada pel color blanc és: $$ \text{blanc}=\frac{12}{16}=\frac34 $$
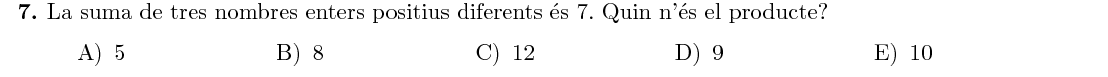 Mostra solució ▾
Mostra solució ▾La única forma de sumar $7$ amb tres nombres naturals diferents és: $$ 7=1+2+4 $$ I el seu producte és $1\cdot2\cdot4=8$.

Hi ha dues zones grises: la primera és la resta entre l'estel més gran i el segon més gran. La segona és la resta entre el segon estel més petit i el més petit. La suma és: $$ A=(16-9)+(4-1)=7+3=10\text{ cm}^2 $$
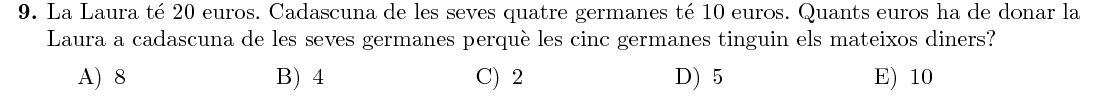 Mostra solució ▾
Mostra solució ▾Si Laura dóna $x$ euros a cada germana, per tal que totes tinguin els mateixos diners cal que: $$ 20-4x=10+x \quad\Rightarrow\quad 5x=10 \quad\Rightarrow\quad x=2 $$ I totes es queden amb $12$ euros.
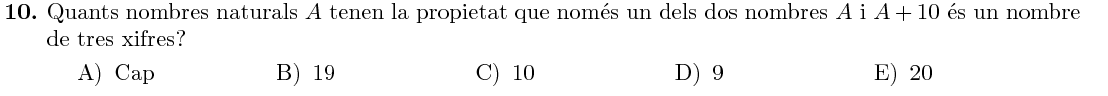
Tenim dues opcions: que $A$ sigui un nombre de tres xifres i $A+10$ no ho sigui, o que $A+10$ sigui de tres xifres però $A$ no. Per cada cas, tenim $10$ opcions diferents:
- $A={990,\ 991,\ 992,\ \ldots,\ 999}$. Per qualsevol d'aquests $10$ valors de $A$, $A+10$ tindrà quatre xifres.
- $A={90,\ 91,\ 92,\ \ldots,\ 99}$. Per aquests $10$ valors de $A$, $A+10$ tindrà tres xifres.
En total, hi ha $20$ nombres naturals $A$ amb aquesta propietat.
Qüestions de 4 punts
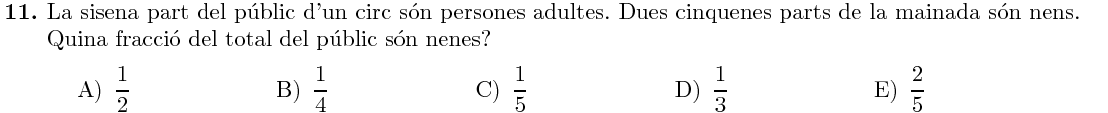
Si $\frac16$ són adults, $\frac56$ són nens i nenes. D'aquests, $\frac25$ són nens i $\frac35$ són nenes. En total: $$ P_{\text{nenes}}=\frac56\cdot\frac35=\frac{15}{30}=\frac12 $$
 Mostra solució ▾
Mostra solució ▾Només hi ha dues sumes que tenen un resultat múltiple de $5$: $$ 3+12=15,\quad8+12=20 $$ El sumand repetit a les dues sumes és $12$, i per tant aquestà serà l'edat de la Neus. Llavors, la Sara i la Joana tindran $3$ o $8$ anys cadascuna (els altres sumands de les dues sumes anteriors). Finalment, la Rita tindrà el número d'anys que queda: $14$ anys.

Anomenem $x$ el nombre total de participants. Segons l'enunciat, hi ha $0.35x$ dones i $252 + 0.35x$ homes. En total: $$ (252+0.35x) + 0.35x = x $$ Resolem l'equació: $$ 252=0.3x\quad\Rightarrow\quad x=\frac{252}{0.3}=840 $$
 Mostra solució ▾
Mostra solució ▾Anomenem $a,b,c$ els tres nombres que faltes (d'esquerra a dreta). Llavors tenim les equacions: $$ \begin{cases} 3&+&a&+&b&+&c&+&4&=&35 \\ 3&+&a&+&b&&&&&=&22\\ &&&&b&+&c&+&4&=&25 \end{cases} $$ Si a la primera equació li restem les altres dues, tenim: $$ -b=35-22-25=-12\quad\Rightarrow\quad b=12 $$ Substituint a la segona i tercera equacions, deduim que: $$ 3+a+12=22\quad\Rightarrow\quad a=7 $$ $$ 12+c+4=25\quad\Rightarrow\quad c=9 $$ El producte dels nombres dels quadrats grisos $(a,c)$ és: $$ a\cdot c=7\cdot9=63 $$
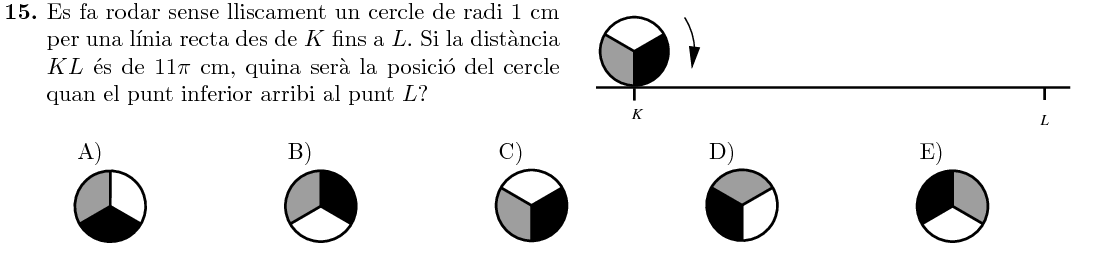 Mostra solució ▾
Mostra solució ▾El cercle pega una volta sencera cada $2\pi\text{ cm}$. Després de $11\pi\text{ cm}$ haurà pegat $5$ voltes completes (es trobarà en la posició inicial), i després pegarà mitja volta. Llavors, la posició final serà la E.

Si comencem posant un nombre senar a dalt de tot, a sota d'ell ha d'haver-hi un senar i un parell: $$ \begin{array}{ccc} &S&\\ S&&P\\ \end{array} $$ Com a molt, podrem posar dos nombres senars a sota: $$ \begin{array}{ccccc} &&S&&\\ &S&&P&\\ P&&S&&S\\ \end{array} $$ I a sota del tot, podem posar $3$ senars com a molt: $$ \begin{array}{ccccccc} &&&S&&&\\ &&S&&P&&\\ &P&&S&&S&\\ S&&S&&P&&S\\ \end{array} $$ En total, hem posat $7$ nombres senars.
Mai podrem posar $8$ nombres senars, perquè llavors només en tindríem $2$ de parells. Si provem, veiem que necessàriament hi ha d'haver algun dels dos nombres parells a la base i és impossible evitar que n'acaben apareixent més de $2$.

L'àrea ombrejada és la de dos triangles de base $1$ i altura $4$ (la meitat del costat del quadrat). Per tant, en total mesura: $$ A=2\cdot\left(\frac12\cdot1\cdot4\right)=4\text{ cm}^2 $$
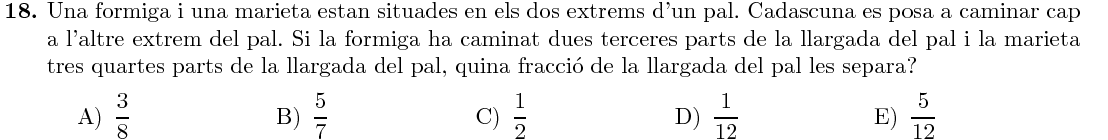 Mostra solució ▾
Mostra solució ▾Observem que la marieta ha caminat $\frac34$ de la longitud del pal, però començava des del final. Per tant es troba a la posició $1-\frac34=\frac14$.
La separació és: $$ \text{separació} = \frac23-\frac14=\frac{8-3}{12}=\frac5{12} $$
 Mostra solució ▾
Mostra solució ▾Dels $7$ dies de la setmana, pot triar: $$ \begin{array}{cccc} (1, 3),& (1, 4),& (1, 5),& (1, 6), \\ (2, 4),& (2, 5),& (2, 6),& (2, 7),\\ (3, 5),& (3, 6),& (3, 7),\\ (4, 6),& (4, 7),\\ (5, 7) \end{array} $$ En total, pot configurar $14$ calendaris diferents.

La única forma d'omplir la graella és (després ho justifiquem): $$ \begin{array}{ccc} 2&3&2\\ 3&2&3\\ 2&3&2 \end{array} $$ Totes les parelles de caselles contigües sumen $5$ . En total, tenim cinc dosos i quatre tresos, i la suma és: $$ S=5\cdot2+4\cdot3=10+12=22 $$ Per justificar com hem omplit la graella, anemenem $x$ el nombre que va a la dreta del $2$ original, i $y$ el nombre a sota de $x$ (a l'esquerra del $3$). Llavors, sabem que $2+x=x+y=y+3$. De la igualtat esquerra deduïm que $y=2$, i de la igualtat dreta que $x=3$. Si repetim el procediment, veiem que al final la taula quedarà plena de dosos i tresos alternativament.
Qüestions de 5 punts

Observem primer que com a mínim la suma haurà de valer $91^\circ$. Si fóra $90^\circ$ o menys, el tercer angle mesuraria $180-90=90^\circ$, i per tant seria el més gran dels tres, cosa que no pot ser.
Finalment, comprovem que la suma sí que pot ser $91^\circ$, cosa que ocorreria amb un triangle d'angles $(1^\circ, 89^\circ, 90^\circ)$.
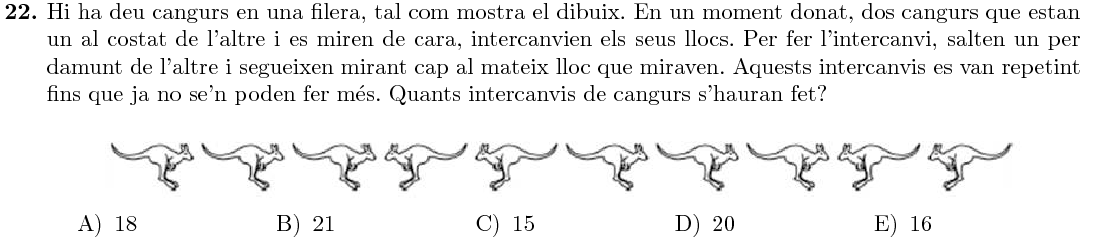
Esquematitzem la figura posant fletxes enlloc de cangurs: $$ \begin{array}{ccccccccc} \rightarrow &\rightarrow& \rightarrow&\leftarrow& \leftarrow&\rightarrow& \rightarrow& \rightarrow& \leftarrow& \leftarrow \end{array} $$ Cada fletxa avançarà totes les que tingui en la direcció contrària més enllà de la direcció cap on apunta: $$ \begin{array}{ccccccccccc} \rightarrow&\rightarrow& \rightarrow&\leftarrow& \leftarrow&\rightarrow& \rightarrow& \rightarrow& \leftarrow& \leftarrow \\ 4&4&4&3&3&2&2&2&6&6 \end{array} $$ La suma és: $$ 4+4+4+3+3+2+2+2+6+6=36 $$ Fixem-nos, però, que hem comptat cada salt dues vegades, i per tant en total s'han fet $36\div2=18$ intercanvis.

Per obtindre dues sumes iguals, haurem de sumar $5$ i $2$ a parelles de nombres que tinguen una diferència de $3$. Com a molt, podem trobar tres d'aquestes parelles: $$ (1,4),\quad (2,5),\quad(3,6) $$ En total, tindrem $9-3=6$ sumes diferents.

Abans que el cotxe arribe (en $60$ minuts), hauran arribat els següents busos que han sortit en $3,6,\ldots$ minuts, els quals hauran arribat en: $$ 38,\ 41,\ 44,\ 47,\ 50,\ 53,\ 56,\ 59\ \text{ minuts} $$ En total, l'han avançat $8$ autobusos.

En primer lloc, observem que el quadrat gris d'enmig té un costat que és $\frac35$ del costat del quadrat gran (mesura $3$ de les $5$ diagonals dels quadradets petits inclinats). Per tant, l'àrea entre els dos quadrats és: $$ A_{\text{fora quadrat interior}}=1-\left(\frac35\right)^2=1-\frac9{25}=\frac{16}{25} $$ Pel que fa a la resta, es troba dividida a parts iguals entre els quadradets grisos i l'espai blanc. Per tant, el percentatge blanc és la meitat de $\frac{16}{25}$: $$ A_{\text{blanc}}=\frac{16}{25}\cdot\frac12=\frac{8}{25}=\frac{32}{100}=32\% $$
 Mostra solució ▾
Mostra solució ▾Vegem com continua la llista, fins trobar un patró: $$ 2,3,\underbrace{6,8,8,4,2,8},\underbrace{6,8,8,4,2,8},\ldots $$ Buscarem la posició $2015$ a partir de la posició $3$, en què es comença a repetir una seqüència de longitud $6$. Calculem el residu de la divició per $6$: $$ 2015=335\cdot6+5 $$ Per tant, a la posició $2017$ hi ha el $5\text{è}$ nombre del cicle: un $2$.
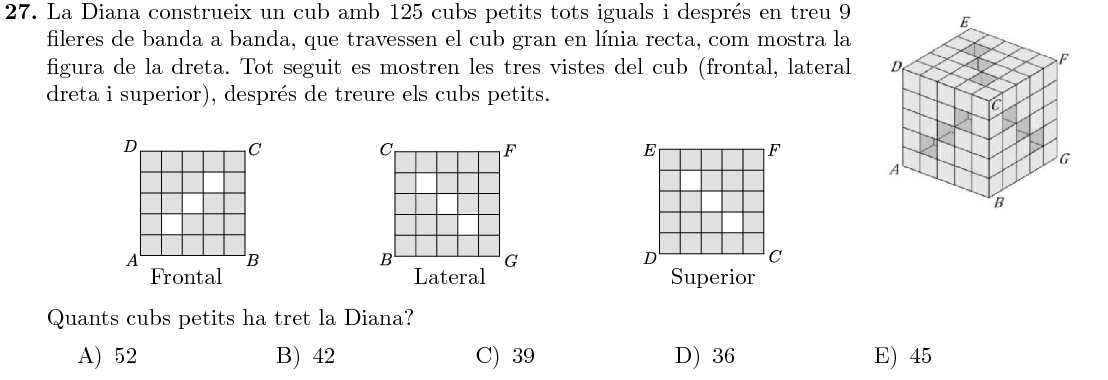
Comencem comptant els $3$ cubets que ha tret de la superfície de cada cara. En total això són $6\cdot3=18$ cubets.
Pel que fa al cub $3\times3\times3$ interior, mirem en detall què passa a cada capa, per no descomptar-nos:
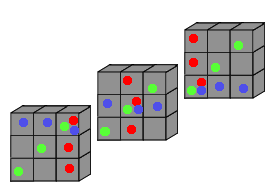
Al cub interior Diana ha tret $7\cdot3=21$ cubets.
En total, ha tret $$ 18+21=39\text{ cubets} $$
 Mostra solució ▾
Mostra solució ▾Els corredors van a una velocitat de: $$ v_A=\frac{720}{4}=180\text{ m/min} $$
$$ v_B=\frac{720}{5}=144\text{ m/min} $$
Tornaran a coincidir després de $t$ minuts, en què entre els dos hauran recorregut $720\text{ m}$: $$ 180t+144t=720\quad\Rightarrow\quad324t=720\quad\Rightarrow\quad t=\frac{20}{9} $$ En aquest temps, el segon corredor haurà recorregut: $$ d_B=144\cdot\frac{20}{9}=320\text{ m} $$
 Mostra solució ▾
Mostra solució ▾Els punts que marca en Simó són: $$ \frac{1}{60},\ \frac{2}{60},\ \frac{3}{60},\ \cdots, \frac{59}{60} $$ I els que marca Bàrbara són: $$ \frac{1}{36},\ \frac{2}{36},\ \frac{3}{36},\ \cdots, \frac{35}{36} $$ Recordem també les factoritzacions en nombres primers de $36$ i $60$: $$ 36=2^2\cdot3^2 $$
$$ 60=2^2\cdot3\cdot5 $$
Per tal que dues fraccions (una de cada llista) siguen iguals, les primeres han d'eliminar el factor $5$ del denominador (tenint un $5$ al numerador), i les segones han d'eliminar un $3$ del denominador (tenint un $3$ al numerador).
Entre l'$1$ i el $59$, hi ha $11$ múltiples de $5$, i entre l'$1$ i el $35$ hi ha $11$ múltiples de $3$, que ens donaran les $11$ coincidències en les marques:
$$ \begin{array}{ccccc} \text{Simó}&&&&\text{Bàrbara}\\ \frac{5}{60}&=&\frac1{12}&=&\frac{3}{36}\\ \frac{10}{60}&=&\frac2{12}&=&\frac{6}{36}\\ \cdots&&\cdots&&\cdots\\ \frac{55}{60}&=&\frac{11}{12}&=&\frac{33}{36} \end{array} $$
En total, doncs, hi haurà:
$$ \text{marques}=59+35-11=83 $$
La qual cosa suposa que el cordill es tallarà en:
$$ \text{trossos}=83+1=84 $$

Podem dividir la figura en tres zones de colors diferenciats:
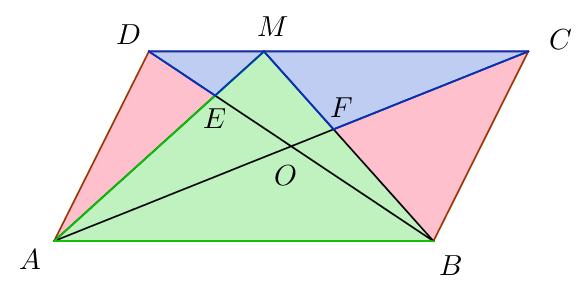
En aquesta figura, sabem que el triangle verd, $\triangle ABM$, té una àrea de $\frac{S}2$, ja que és un triangle amb la mateixa base i altura que el paral·lelogram. A més, els triangles vermells tenen una àrea de $\frac{S}3$, tal com diu l'enunciat. Per tant, els triangles blaus, $\triangle DEM$ i $\triangle FCM$ sumen una àrea que és la diferència respecte a l'àrea total: $$ A_{\triangle DEM}+A_{\triangle FCM} = S - \frac{S}{2} - \frac{S}3 = \frac{S}6 $$ D'altra banda, fixem-nos en el triangle superior $\triangle DOC$, que té una àrea que mesura $\frac{S}4$, perquè està delimitat per les dues diagonals (mateixa base que el paral·lelogram i la meitat d'altura):
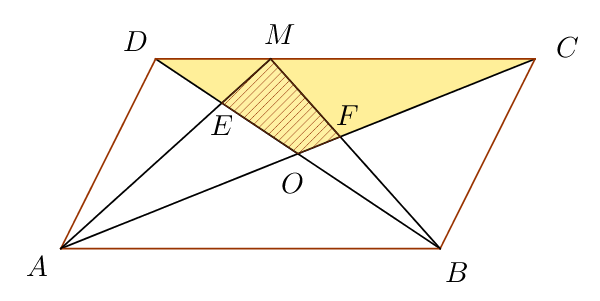
I l'àrea del quadrilàter $\square EOFM$ és la resta entre $A_{\triangle DOC}$ i els dos triangles que hem calculat abans ($\triangle DEM$ i $\triangle FCM$): $$ A_{\square EOFM} = A_{\triangle DOC} - (A_{\triangle DEM} + A_{\triangle FCM}) = \frac{S}4 - \frac{S}6 = \frac{S}{12} $$ Finalment, hem vist que l'àrea del quadrilàter és $A_{\square EOFM}=\frac{S}{12}$.