Solucions del Cangur 2017 a Catalunya: 2n de batxillerat
Descobreix la Contrarellotge matemàtica, el portal de concursos matemàtics online.
Ací teniu el recull de solucions del Nivell de 2n de batxillerat del Cangur de Catalunya de 2017. Els enunciats estan extrets del primer model d'examen del pdf d'enunciats. Les solucions estan amagades (cal fer clic per mostrar-les) perquè és recomanable pensar detingudament cada problema abans de mirar la solució que jo proposo!
Podeu accedir a les qüestions directament:
- Qüestions de 3 punts: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10.
- Qüestions de 4 punts: 11, 12, 13, 14, 15, 16, 17, 18, 19, 20.
- Qüestions de 5 punts: 21, 22, 23, 24, 25, 26, 27, 28, 29, 30.
Els enunciats del Cangur són propietat de la Societat Catalana de Matemàtiques i Le Kangourou sans Frontières.
Qüestions de 3 punts
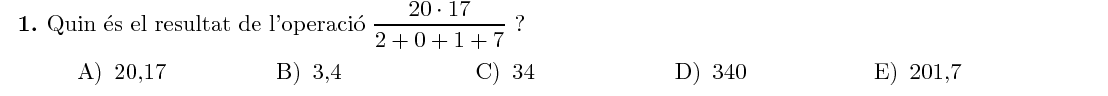
Operem: $$ \frac{20\cdot17}{2+0+1+7}=\frac{20\cdot17}{10}=\frac{20}{10}\cdot17=2\cdot17=34 $$
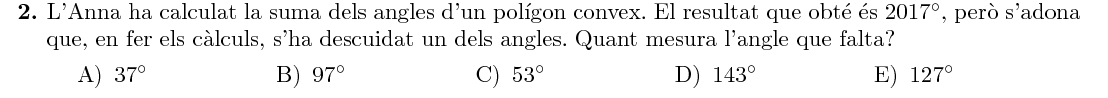 Mostra solució ▾
Mostra solució ▾La suma dels angles d'un polígon convex sempre és un múltiple de $180$. Vegem quin és el següent múltiple de $180$ després de $2017$: $$ 2017=11\cdot180 + 37 $$ Per tant, l'angle que falta mesura: $$ \text{angle} = 180-37=143^\circ $$
 Mostra solució ▾
Mostra solució ▾A simple vista es pot veure que no es pot fer eliminant només $2$ ponts, però sí eliminant-ne $3$:

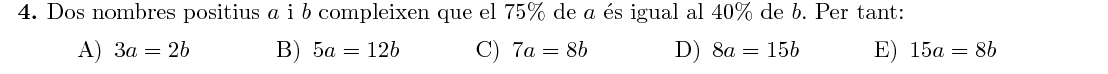
Podem expressar la igualtat com: $$ 0.75a=0.4b\quad\Rightarrow\quad\frac34a=\frac25b\quad\Rightarrow\quad15a=8b $$
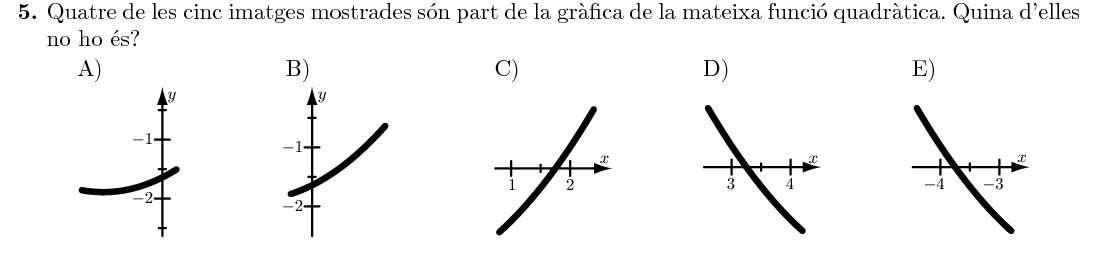 Mostra solució ▾
Mostra solució ▾La gràfica $A$ ens mostra una paràbola que comença a créixer a prop de $x=0$. La gràfica $B$ és compatible amb la corba d'$A$. La gràfica $C$ ens mostra una corba creixent al voltant de $x\in(1,2)$. La gràfica $E$ ens mostra una gràfica decreixen al voltant de l'interval $x\in(-4,-3)$, cosa que també és compatible.
En canvi, la gràfica $D$ ens mostra una corba que decreix a l'interval $(3,4)$, cosa que no coincideix amb les altres quatre gràfiques.
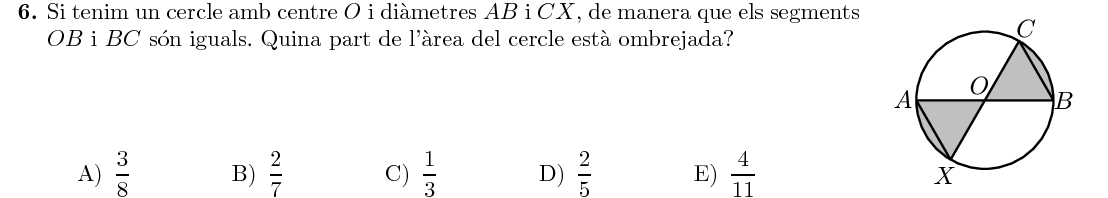
Com els segments $OB$ i $BC$ són iguals, els dos triangles seran equilàters, i per tant cada sector circular equival a $\frac16$ del cercle. En total, l'àrea ombrejada és la part del cercle: $$ A_{\text{ombrejada}} = \frac16+\frac16=\frac13 $$
 Mostra solució ▾
Mostra solució ▾Els costats del triangle són les sumes dels radis dos a dos: $$ \triangle = (3+2, 3+1, 2+1) = (5, 4, 3) $$ De fet, es tracta d'un triangle rectangle, ja que es compleix el Teorema de Pitàgores: $$ 3^2+4^2=5^2 $$ L'àrea, per tant, és la meitat del producte dels dos catets: $$ A=\frac12\cdot3\cdot4=6 $$
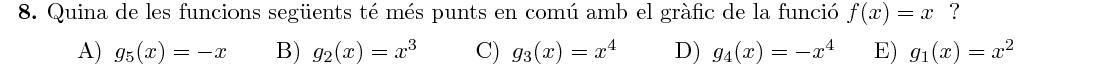 Mostra solució ▾
Mostra solució ▾Calculem les solucions: $$ \begin{array}{lcl} g_5(x)=-x=x &\Rightarrow& x=0 \\ g_2(x)=x^3= x &\Rightarrow& x={0, 1, -1}\\ g_3(x)=x^4=x &\Rightarrow& x={0,1}\\ g_4(x)=-x^4= x& \Rightarrow& x={0,-1}\\ g_1(x)=x^2= x &\Rightarrow& x={0,1}\\ \end{array} $$ Per tant, $g_2$ és la funció amb més punts en comú amb $f$.

Calculem la probabilitat de triar una bola blava de cada capsa:
$$ P_A=\frac{10}{10+8}=\frac{5}{9} $$ $$ P_B=\frac{6}{6+4}=\frac{3}{5} $$ $$ P_C=\frac{8}{8+6}=\frac{4}{7} $$ $$ P_D=\frac{7}{7+7}=\frac{1}{2} $$ $$ P_E=\frac{12}{12+9}=\frac{4}{7} $$
La major d'aquestes fraccions és $P_B=\frac35$. Ho podem comprovar triant un denominador comú: $$ P_B=\frac35=\frac{27}{45} > \frac{25}{45} = \frac{5}{9} = P_A $$ $$ P_B=\frac35=\frac{21}{35} > \frac{20}{35} = \frac{4}{7} = P_C=P_E $$ $$ P_B=\frac35=\frac{6}{10} > \frac{5}{10} = \frac{1}{2} = P_D $$
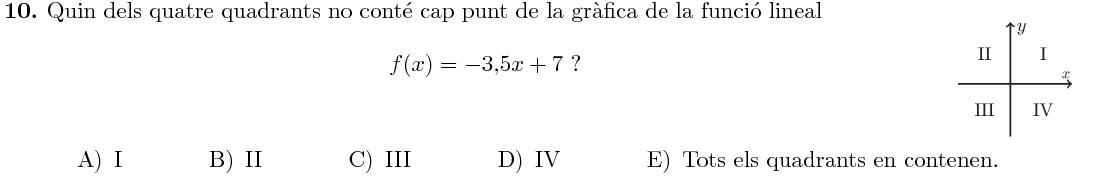
Es tracta d'una recta que no passa per l'origen, per tant no pot ser que passi pels quatre quadrants. Vegem per quins sí que passa: $$ \begin{array}{lclcl} x=-1 &\Rightarrow& f(-1)=3.5+7=10.5&\Rightarrow& (-1, 10.5)\in\text{II} \\ x=1&\Rightarrow& f(1)=-3.5+7=3.5&\Rightarrow& (1, 3.5)\in\text{I} \\ x=3 &\Rightarrow& f(3)=-10.5+7=-3.5&\Rightarrow& (3, -3.5)\in\text{IV} \end{array} $$
L'únic quadrant pel que no passa és pel $\text{III}$.
Qüestions de 4 punts
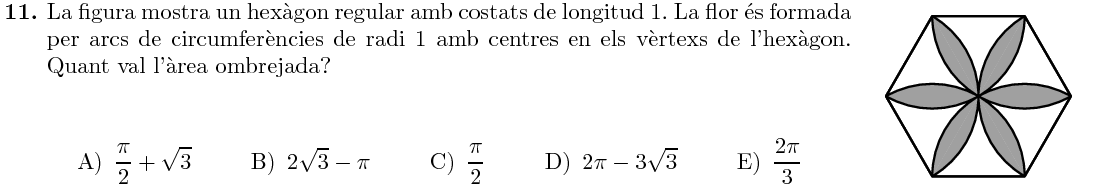
En primer lloc, observem que podem dividir els pètals en dos de la següent manera:
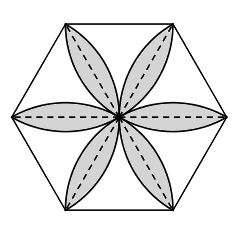
I cada mig pètal es correspon amb l'àrea que queda entre un triangle equilàter i un sector circular:
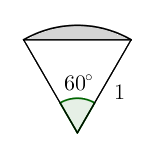
Calculem ara l'àrea del triangle i la del sector circular per fer la resta. Pel Teorema de Pitàgores, esbrinem l'altura del triangle: $$ h^2+\left(\frac12\right)^2=1^2\quad\Rightarrow\quad h^2=\frac34\quad\Rightarrow\quad h=\frac{\sqrt{3}}2 $$ Per tant, l'àrea del triangle és: $$ A_{\text{triangle}}=\frac12\cdot1\cdot\frac{\sqrt3}2=\frac{\sqrt3}{4} $$ El sector circular té una àrea que és la sisena pert de la del cercle: $$ A_{\text{sector circular}} = \frac16\cdot\pi\cdot1^2=\frac\pi6 $$ Per tant, l'àrea de mig pètal és: $$ A_{\text{mig pètal}} = A_{\text{sector circular}} - A_{\text{triangle}} = \frac\pi6 - \frac{\sqrt3}4 $$ Finalment, l'àrea ombrejada original té $6$ pètals, és a dir, $12$ mitjos pètals: $$ A_{\text{ombrejada}} = 12\cdot A_{\text{mig pètal}} = 12\cdot\left(\frac\pi6 - \frac{\sqrt3}4\right) = 2\pi - 3\sqrt3 $$
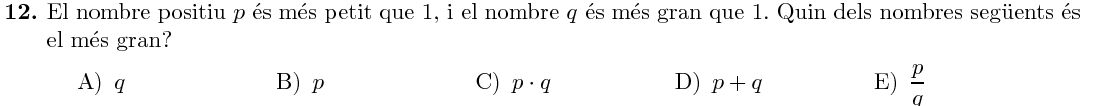 Mostra solució ▾
Mostra solució ▾En ordre decreixent, tenim les següents desigualtats: $$ p+q \quad >\quad q \quad >\quad p\cdot q\quad >\quad p\quad >\quad \frac{p}{q} $$ Per tant, $p+q$ és el més major de tots.

Anomenem $h_A, h_B$ les altures dels cilindres i $r_A,r_B$ els radis de les seues bases. Sabem $1.1r_A=r_B$, i els volums són iguals, per tant: $$ \pi r_A^2h_A = \pi r_B^2h_B \quad\Rightarrow\quad r_A^2h_A = 1.1^2r_A^2h_B \quad\Rightarrow $$
$$ \Rightarrow\quad h_A=1.1^2h_B\quad\Rightarrow\quad \frac{h_A}{h_B}=1.1^2=1.21 $$
És a dir, l'altura del cilindre $A$ és un $21\%$ més llarga que la de $B$.

Cadascun dels $6$ quadrats està en contacte amb $4$ triangles, però estarem contant cada triangle $3$ cops, ja que cada triangle està en contacte amb $3$ quadrats. Per tant: $$ N_{\text{triangles}}=\frac{6\cdot4}3=8 $$
 Mostra solució ▾
Mostra solució ▾La millor opció serà posar una bola negra a cada caixa i totes les blanques en la mateixa caixa. La probabilitat de guanyar serà: $$ P_C=\frac45 + \frac15\cdot\frac16=\frac{25}{30}=\frac56 $$ És fàcil comprovar que totes les altres opcions donen probabilitats més petites: $$ \begin{array}{l} P_A=\frac35\\ P_B=\frac12\\ P_D=\frac15\cdot\frac56=\frac16\\ P_E=\frac45 \end{array} $$
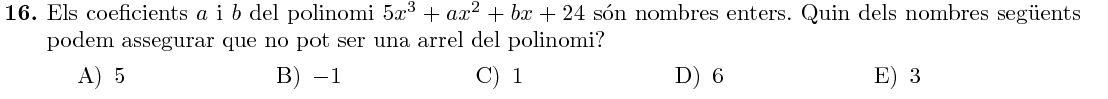 Mostra solució ▾
Mostra solució ▾Si $x$ és una arrel del polinomi, es compleix: $$ \begin{array}{rrllc} & 5x^3+ax^2+bx+24&=&0&\Rightarrow\\ \Rightarrow& 5x^3+ax^2+bx&=&-24 &\Rightarrow\\ \Rightarrow& x(5x^2+ax+b)&= &-24 \end{array} $$ Per tant, $x$ ha de ser un divisor de $-24$, i $5$ és la única opció que no ho és.

El quadrat més gran que podrà formar serà de costat $44$: $$ 44\times44=1936 \text{ fitxes (968 blanques, 968 negres)} $$ Per tant, li sobraran: $$ \begin{array}{rcl} 1009-968 &=& 41\text{ fitxes negres}\\ 1008-968 &=& 40 \text{ fitxes blanques} \end{array} $$

En primer lloc, observem que els nombres contigus tindran paritat diferent (tenen diferència $1$). Per tal que la suma sigui senar, cal que hi hagi un nombre senar de sumands senars. Dels $7$ nombres, per tant, $3$ han de ser senars: hauran de ser $b, d, f$.
Per tant, els nombres $a,c,e,g$ hauran de ser parells. Si $a$ pot ser $286$, també ho podrà ser $g$ per simetria; si $c$ pot ser $286$, també ho podrà ser $e$ per simetria. Provarem si és possible.
Per simplificar, calculem que $286\cdot7=2002$, de manera que ens falten $15$ fins arribar a $2017$. Anotarem cada nombre respecte a 286, i buscarem sumar $15$. Mirem si pot ser que $a=286$: $$ \begin{array}{ccccccccc} a&b&c&d&e&f&g&&\text{suma}\\ 0&1&2&3&4&3&2&&15 \end{array} $$ Provem ara amb $c=286$: $$ \begin{array}{ccccccccc} a&b&c&d&e&f&g&&\text{suma}\\ 2&1&0&1&2&3&4&&13 \end{array} $$ Com a màxim, podem obtenir una suma de $13$, i no podem arribar a $15$.
Per tant, només poden ser $286$ la $a$ i la $g$.
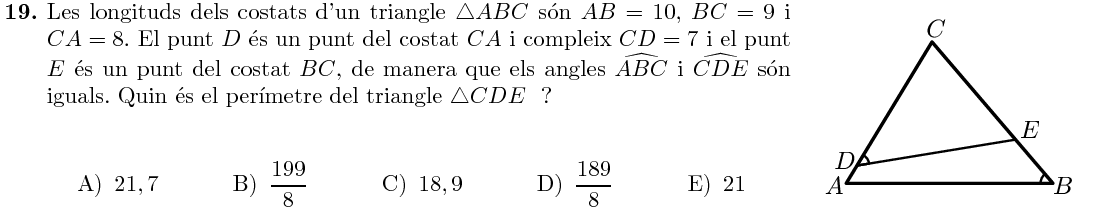
Com els dos triangles $\triangle ABC$ i $\triangle CDE$ comparteixen l'angle $\angle ACB$, i també l'angle de la figura, coincidiran també en el tercer angle, és a dir, són triangles semblants.
Concretament, el costat $CD=7$ es correspon al costat $BC=$9. Per tant, el perímetre serà $\frac79$ del perímetre original:
$$ \text{Perímetre}(\triangle CDE) = \frac79\cdot(8+9+10)=\frac79\cdot 27=21 $$
 Mostra solució ▾
Mostra solució ▾Anomenem $ab$ el nombre, llavors les frases que ha dit Tytti són:
- $a=2$ o $b=2$
- $ab > 50$
- $ab$ és parell
- $ab < 30$
- $ab \mid 3$ (és disible per $3$).
- $a=7$ o $b=7$
Fixem-nos que les afirmacions 2 i 4 són contradictòries. Com de les afirmacions 2, 3, 4 només pot ser falsa una, haurà de ser-ho alguna de les dues. Provem amb aquestes dues opcions.
Si la frase 2 és falsa, també ho serà la 5. Per tant, sabem que les dues xifres seran $2$ i $7$ (afirmacions 1 i 6). Sabem que serà parell (afirmació 3), i per tant ha de ser el $72$. Però això no pot ser perquè hem suposat falsa l'afirmació 2, que deia que seria major que $50$.
Si la frase 4 és falsa, llavors també serà falsa la 1. Per tant, busquem un número major que $50$ (frase 2), parell (frase 3), que tingui un $7$ (frase 6), i divisible per $3$. Com ha de ser parell, el $7$ serà la primera xifra. Les possibles opcions són $70,74,76,78$ (el $72$ no pot ser perquè la frase 1 és falsa). D'aquests, l'únic que és múltiple de $3$ (frase 5) és el $78$.
Finalment, la suma de les xifres de $78$ és $7+8=15$.
Qüestions de 5 punts

Anomenem $x$ un nombre que compleixi la condició anterior, i siga $u$ la seua xifra de les unitats. Llavors, ha de complir la següent condició: $$ \frac{x-u}{10} = \frac{x}{14} $$ Passant els denominadors a l'altra banda, tenim: $$ 14x-14u=10x\quad\Rightarrow\quad 4x=14u\quad\Rightarrow\quad x=\frac72u $$ Com que $u$ és un número entre $0$ i $9$, i $x$ ha de ser múltiple de $14$, només hi ha $2$ possibles valors per $u$: $$ u\in{4,8} $$ Per tant, hi ha $2$ enters positius que ho compleixen. Són: $$ x=14 \quad\rightarrow\quad 1 = 14\div14 $$ $$ x=28 \quad\rightarrow\quad 2 = 28\div14 $$
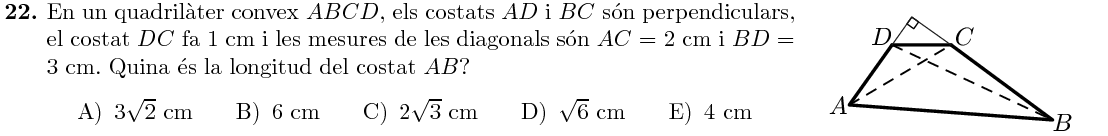
Girem el dibuix per centrar-nos en els triangles rectangles que hi apareixen:
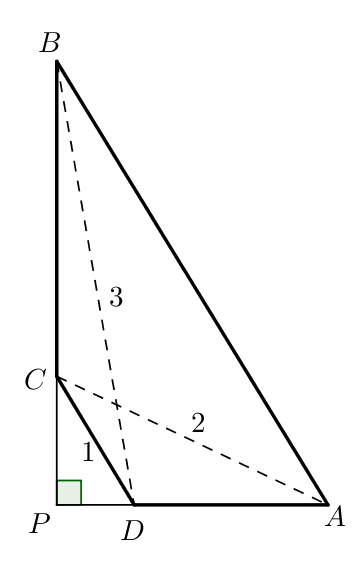
Hem anomenat $P$ el punt d'intersecció dels segments $BC$ i $AD$, que formen un angle recte.
Adonem-nos que tenim quatre triangles rectangles amb què treballar: $\triangle PDC$, el més petit de tots, amb hipotenusa $1$, $\triangle PAC$, el segon més petit, amb hipotenusa $2$. El triangle $\triangle PDB$, amb hipotenusa $3$, i finalment, el triangle $\triangle PAB$, del qual volem esbrinal la hipotenusa, $AB$.
Pel Teorema de Pitàgores sobre el triangle més petit, sabem que: $$ PD^2+PC^2=1^2 $$ Pel Teorema de Pitàgores sobre els dos triangles mitjans, sabem que: $$ PC^2+PA^2=2^2\quad\Rightarrow\quad PA^2=4-PC^2 $$
$$ PD^2+PB^2=3^2\quad\Rightarrow\quad PB^2=9-PD^2 $$
I volem esbrinar el que mesura $AB$, que pel Teorema de Pitàgores compleix: $$ AB^2=PA^2+PB^2 $$ Podem substituir $PA^2$ i $PB^2$ pel que acabem d'aïllar: $$ AB^2=(4-PC^2)+(9-PD^2) = 13- (PC^2+PD^2) $$ Però recordem que pel triangle petit havíem deduït que $PD^2+PC^2=1$, per tant: $$ AB^2=13-1=12 $$ Finalment: $$ AB=\sqrt{12}=2\sqrt{3} $$
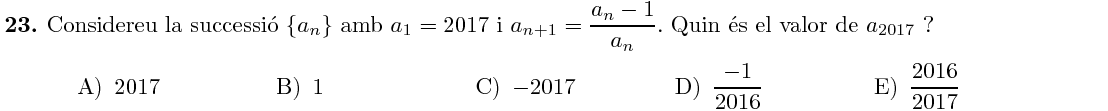 Mostra solució ▾
Mostra solució ▾Vegem com evoluciona la successió en els primers termes: $$ a_1=2017 $$
$$ a_2=\frac{a_1-1}{a_1}=\frac{2016}{2017} $$
$$ a_3=\frac{a_2-1}{a_2}=\frac{\frac{2016}{2017}-1}{\frac{2016}{2017}}=\frac{\frac{-1}{2017}}{\frac{2016}{2017}}=\frac{-1}{2016} $$
$$ a_4=\frac{a_3-1}{a_3}=\frac{\frac{-1}{2016}-1}{\frac{-1}{2016}}=\frac{\frac{-2017}{2016}}{\frac{-1}{2016}}=2017 $$
Hem vist que es repetirà el cicle $(2017, \frac{2016}{2017}, \frac{-1}{2016}, \ldots)$. Per saber quant valdrà $a_{2017}$, calculem el residu de dividir entre $3$: $$ 2017=672\cdot3+1 $$ Per tant, $a_{2017}=a_1=2017$.

Adonem-nos que al tetraedre original li hem tret quatre tetraedres petits, un per cada vèrtex. Per resoldre el problema, calcularem el volum d'aquests tetraedres petits, per exemple, ens podem centrar en el superior.
Pel Teorema de Tales, sabem que l'altura del tetraedre petit serà la meitat que la de l'original. Pel que fa a la base (que és un triangle equilàter), tindrà una base que també serà la meitat, i una altura que també serà la meitat. En resum, el volum serà $\frac12\cdot\frac12\cdot\frac12=\frac18$ de l'original.
Com tenim $4$ d'aquests petits tetraedres, en total hem restat $4\cdot\frac18=\frac12$ del volum original, i per tant el sòlid resultat té un volum d'$\frac12$ del volum original.
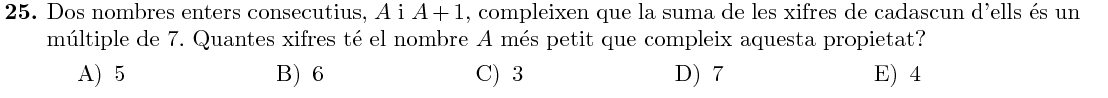
Si la suma de les xifres del nombre $A$ és múltiple de $7$, i la suma de les xifres d'$A+1$ també és múltiple de $7$, això vol dir que la variació en la suma de les xifres entre els dos nombres també serà múltiple de $7$.
Vegem com canvia la suma de les xifres d'un nombre quan li sumem $1$, i si aquesta variació pot ser múltiple de $7$. Anomenarem $d$ aquesta variació en la suma de les xifres:
- Si la xifra de les unitats és menor que $9$, a la suma de les xifres se li suma $d=1$, que no és múltiple de $7$.
- Si el número acaba en $9$, la suma de les xifres varia així: $d=-9+1=-8$. Tampoc múltiple de $7$.
- Si el número acaba en $99$: $d=-9-9+1=-17$. Tampoc múltiple de $7$.
- Si el número acaba en $999$: $d=-9-9-9+1=-26$. Tampoc múltiple de $7$.
- Si el número acaba en $9999$: $d=-9-9-9-9+1=-35$. Que és multiple de $7$!
Per tant, sabem que com a mínim, $A$ acabarà en $9999$. Per tal que $A$ sigui múltiple de $7$ li haurem d'afegir una xifra al davant de tot, que haurà de ser un $6$: $$ \begin{array}{rcl} A=69\,999&\rightarrow&6+9+9+9+9=42\mid7\\ A+1=700\,000&\rightarrow&7+0+0+0+0+0=7\mid7\\ \end{array} $$ Per tant, l'$A$ més petit que compleix aquesta propietat té $5$ xifres.

Si considerem els daus com a diferents, podem obtindre un total de $4^4=256$ resultats diferents. Com cada dau oculta només una cara, per tal que no poguem compondre el número $2017$ (que té totes les xifres diferents), és necessari que quedi oculta la mateixa xifra als quatre daus. Per tant, hi ha $4$ tirades en què no podrem compondre el $2017$ (una per cada xifra). Llavors, la probabilitat que busquem és: $$ P=\frac{256-4}{256}=\frac{252}{256}=\frac{63}{64} $$
 Mostra solució ▾
Mostra solució ▾Anomenem $x$ el nombre que va a la casella central. Llavors, podem omplir la graella, per exemple, amb els següents nombres: $$ \begin{array}{ccc} x&x+1&x\\ x+1&x&x+1\\ x&x+1&x\\ \end{array} $$ Restem $x$ a cada casella, i ho podem denotar com: $$ \begin{array}{ccc} 0&1&0\\ 1&0&1\\ 0&1&0\\ \end{array} $$ Llavors, la suma del quadrat serà $9x+4$. Busquem quant hauria de sumar el quadrat si $x$ és cadascuna de les opcions: $$ \begin{array}{ccl} x=56&\Rightarrow&500-9\cdot56=-4\\ x=57&\Rightarrow&500-9\cdot57=-13\\ x=54&\Rightarrow&500-9\cdot54=14\\ x=50&\Rightarrow&500-9\cdot50=50\\ x=55&\Rightarrow&500-9\cdot55=5\\ \end{array} $$ És fàcil comprovar que podem obtindre una solució per al primer cas, $x=56$, amb la matriu: $$ \begin{array}{rrr} 0&-1&0\\ -1&0&-1\\ 0&-1&0\\ \end{array} $$
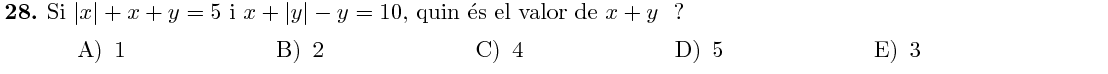 Mostra solució ▾
Mostra solució ▾Provarem suposant que $x$ és negatiu, i després provarem suposant que és positiu si no trobem la solució.
Si $x$ és negativa, $|x|=-x$. Per la primera equació, llavors, deduim que: $$ -x+x+y=5\quad\Rightarrow\quad y=5 $$ Per la segona equació deduim que $x=10$, cosa que no pot ser perquè havíem suposat que $x$ seria negativa.
Si $x$ és positiva, sabem que $|x|=x$, i les equacions queden: $$ \begin{cases} 2x+y&=&5\\ x+|y|-y&=&10 \end{cases} $$ Suposem ara que $y$ és positiva. Llavors, $|y|=y$. De la segona equació deduim que: $$ x+y-y=x=10\quad\Rightarrow\quad2\cdot10+y=5\quad\Rightarrow\quad y=-15\ !! $$ Això no pot ser, perquè havíem suposat que la $y$ seria positiva.
Finalment, suposem que la $y$ és negativa, i per tant $|y|=-y$. Les equacions queden: $$ \begin{cases} 2x+y&=&5\\ x-2y&=&10 \end{cases} $$ I ja podem resoldre el sistema d'equacions: $$ \begin{array}{lll} & x=10+2y\quad\Rightarrow\\ \Rightarrow&2\cdot(10+2y)+y=5\quad\Rightarrow\\ \Rightarrow&20+5y=5\quad\Rightarrow\\ \Rightarrow& y=-3 \end{array} $$ Tenim doncs que: $$ x=10+2y=10+2\cdot(-3)=4 $$ I la suma és: $$ x+y=4-3=1 $$
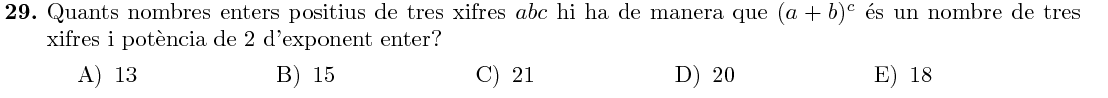 Mostra solució ▾
Mostra solució ▾Només hi ha tres potències de $2$ de tres xifres: $$ {2^7=128,\quad 2^8=256,\quad 2^9=512 } $$ Comptem per separat quantes formes tenim d'obtenir cadascun d'aquests nombres.
Pel que fa a $2^7=128$, l'exponent $c$ haurà de ser $7$. Per tant, s'ha de complir que $a+b=2$. Per tal que $abc$ sigui de tres xifres, a més, cal que $a>0$. Per tant, les opcions que hi ha són: $$ c=7\quad\Rightarrow\quad a+b=2 \quad\Rightarrow\quad (a,b)={(1, 1),\ (2, 0)} $$ Pel que fa a $2^9=512$, ens trobem en un cas com l'anterior, en què $c=9$: $$ c=9\quad\Rightarrow\quad a+b=2\quad\Rightarrow\quad (a,b)={(1, 1),\ (2, 0)} $$ Però també pot ser que $c=3$ i $a+b=2^3=8$: $$ c=3\quad\Rightarrow\quad a+b=8\quad\Rightarrow\quad (a,b)={(1, 7),\ (2, 6),\ \ldots,\ (7, 1),\ (8,0)} $$ En el cas de $2^8=256$, tenim més casos. $c$ pot ser $8$, però també pot ser $4$ o $2$, si la suma $a+b$ és $4$ o $16$. Per tant, les opcions són: $$ \begin{array}{lllll} c=8 & \Rightarrow & a+b=2 & \Rightarrow & (a,b)={(1, 1),\ (2, 0)}\\ c=4 & \Rightarrow & a+b=4 & \Rightarrow & (a,b)={(1, 3),\ (2, 2),\ (3, 1),\ (4,0)}\\ c=2 & \Rightarrow & a+b=16 & \Rightarrow & (a,b)={(7, 9),\ (8, 8),\ (9, 7)} \end{array} $$ En total, hi ha: $$ N=2+2+8+2+4+3=21\text{ opcions} $$

Vegem què passa amb els habitants del banquet. Si un d'ells diu la veritat, llavors al seu voltant en tindrà un de cada mena: $$ \cdots V\ V\ M\cdots $$ Si continuem completant, hem de posar un mentindre a l'esquerra per tant que el que hi ha a l'esquerra digui la veritat. A la dreta, hem de posar algú que diu la veritat per tal que el que hi ha menteixi: $$ \cdots M\ V\ V\ M\ V \cdots $$ Podem continuar completant: $$ \cdots V\ M\ V\ V\ M\ V \ V\cdots $$ Veiem que es repeteix un patró: $\frac23$ dels membres del banquet diuen la veritat.
Fem que el banquet siga tan petit com siga possible, és a dir, amb $1002$ habitants, dels quals $\frac23\cdot1002=668$ diuen la veritat.
La resta d'habitants, en el millor dels casos, diran tots la veritat, i seran $2017-1002=1015$.
Com a màxim, el nombre de no mentiders a l'illa serà: $$ N_{\text{no mentiders}}=668+1015=1683 $$