En primer lloc comptem de quantes maneres podem col·locar les lletres $U$. A la primera fila va una lletra $U$, a una de les $3$ caselles. La segona $U$ va a la segona fila, però només pot anar a una de dues caselles (no pot estar a la mateixa columna que la primera lletra $U$). Per tant, hi ha:

$$3\cdot2=6$$

formes de col·locar les lletres $U$.

La resta de lletres de $SUDOKU$, és a dir, $S,D,K,O$ són diferents. Les haurem de situar a les quatre caselles lliures. Hi ha tantes maneres diferents de fer-ho com permutations de les lletres $SDKO$, és a dir, $4!$. En total, hi ha:

$$6\cdot 4!=6\cdot 24=144$$

formes d'escriure $SUDOKU$ tal com demana l'enunciat, i la solució és la E.

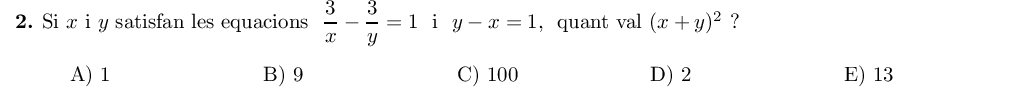
En primer lloc operem amb $(x+y)^2$:

$$(x+y)^2 = x^2 + 2xy + y^2 = x^2 - 2xy + y^2 + 4xy = (y-x)^2 + 4xy$$

Per la segona equació de l'enunciat sabem que $y-x=1$, per tant:

$$(x+y)^2 = 1^2 + 4xy$$

Ara, començant amb la primera equació de l'enunciat:

$$\frac3x - \frac3y = 1 \quad \Rightarrow \quad \frac{3y-3x}{xy} = 1 \quad \Rightarrow \quad 3y-3x = xy$$

Com que $y-x=1$, tenim que:

$$xy = 3y-3x = 3(y-x) = 3$$

Llavors, com volíem saber:

$$(x+y)^2 = 1 + 4xy = 1 + 4\cdot 3 = 13$$

I la solució és la E.

En primer lloc fixem-nos que tots els nombres primers són senars excepte un: el $2$.

Albert escriu una quantitat parella de nombres primers, i la suma és senar. Si tots els nombres primers que ha escrit fóssin senars, la suma seria parella, de manera que entre els nombres que ha escrit hi és el $2$.

Blanca ha escrit una quantitat senar de nombres primers, i la suma és parella. Si només hagués escrit nombres primers senars, la suma seria senar, de manera que ha d'haver escrit el número $2$.

De manera que tant per l'Albert com per la Blanca, els productes de nombres contenen el $2$ i per tant el resultat és parell. La solució és la D.

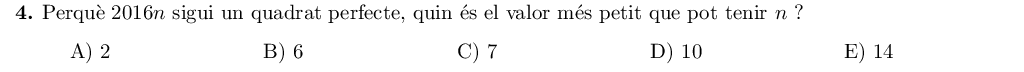
Per ser un quadrat perfecte, en la descomposició en factors primers tot els factors han d'estar elevats a un exponent parell. La descomposició de $2016$ és:

$$2016=2^5\cdot 3^2\cdot 7$$

Per tal que el producte siga un quadrat perfecte, hem de multiplicar com a mínim per $2\cdot 7=14$, de manera que:

$$2016\cdot 14=2^6\cdot 3^2\cdot 7^2=(2^3\cdot 3\cdot 7)^2$$

I la solució és la E.

Dilluns, dimarts i dimecres, el bodeguer ven $6$ dels $30$ litres de la bóta i la reompli d'aigua, és a dir, multiplica per $1-\frac{6}{30}=\frac{4}{5}$ la quantitat de vi que conté la bóta. Com ho fa $3$ cops, al final de vi en queda:

$$30\cdot \left(\frac45\right)^3 = 30\cdot \frac{64}{125} = 15,36$$

La quantitat d'aigua que hi ha és la diferència: $30-15,36=14,64$, i la solució és la C.

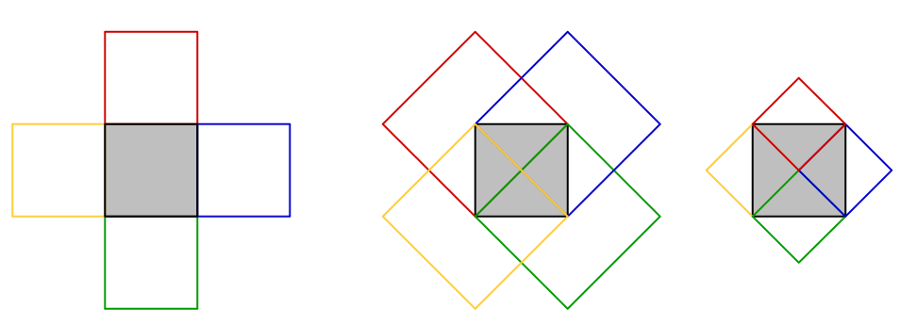
En total hi ha $12$ quadrats diferents, com podem veure a la figura següent, i la solució és la C.

Com que no sabem quina proporció dels $200$ € és deguda al gas i a l'electricitat, no podrem deduir el preu de la propera factura.

Per exemple, si tota la factura fós deguda al gas, hauria de pagar $204$ €, i si fós tota deguda a l'electricitat, n'hauria de pagar $208$. Com l'enunciat no ens dóna més informació, no ho podem saber i la solució és la E.

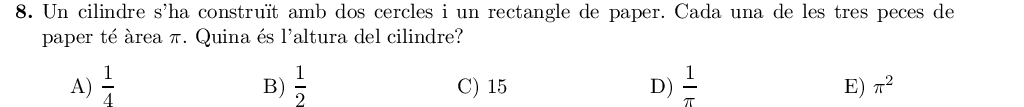
L'àrea dels cercles és $\pi$, i per la fórmula de l'àrea d'un cercle $(\pi r^2)$ podem deduir que el radi és $r=1$. La longitud de la circumferència serà doncs $2\pi$ (per la fórmula $2\pi r$).

Anomenem els dos costats diferents del rectangle base i altura $(b, h)$, segons si es troben a les bases del cilindre o no. La base del rectangle coincideix amb el perímetre dels cercles, és a dir, $b=2\pi$. Sabem que l'àrea del rectangle és $\pi$, per tant:

$$A_{rectangle}=b\cdot h \quad \Rightarrow \quad \pi = 2\pi\cdot h \quad \Rightarrow \quad h = \frac12$$

I la solució és la B.

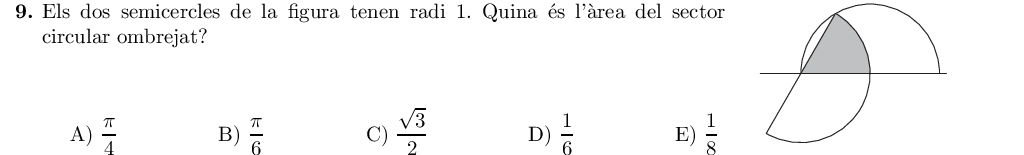
Els dos semicercles tenen radi $1$, i com es pot veure a la figura, els tres segments marcats mesuren $1$, de manera que formen un triangle equilàter i per tant el sector circular ombrejat mesura $60^\circ$.

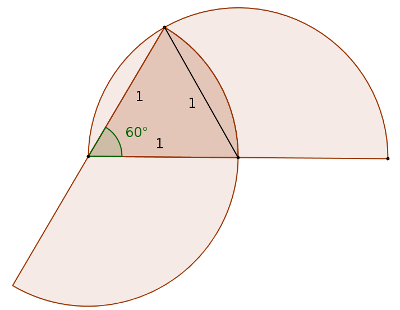
Així doncs, es tracta d'una sisena part del cercle, $60^\circ$ de $360^\circ$, i per tant l'àrea és:

$$A=\frac16\cdot \pi\cdot 1^2 = \frac{\pi}{6}$$

I la solució és la B.

Comencem resolent el sistema:

$$x = \frac{3 \pm \sqrt{3^2-4}}{2} = \frac{3 \pm \sqrt5}{2}$$ $$a = \frac{3 + \sqrt5}{2}, \quad b = \frac{3 - \sqrt5}{2}$$

LLavors, tenim que:

$$a^3+b^3 = \left(\frac{3 + \sqrt5}{2}\right)^3 + \left(\frac{3 - \sqrt5}{2}\right)^3 =$$ $$= \frac{(3+\sqrt5)^3 + (3-\sqrt5)^3}{8}$$

Per fer la suma $(3+\sqrt5)^3 + (3-\sqrt5)^3$, tinguem en compte que:

$$(a+b)^3 = a^3 + 3a^2b + 3ab^2 + b^3$$ $$(a-b)^3 = a^3 - 3a^2b + 3ab^2 - b^3$$

I la suma és:

$$(a+b)^3 + (a-b)^3 = 2a^3 + 6ab^2$$

Per tant:

$$(3+\sqrt5)^3 + (3-\sqrt5)^3 = 2\cdot 3^3 + 6\cdot 3\cdot \sqrt{5}^2 = 54 + 18\cdot 5 = 144$$

En definitiva, tenim que:

$$a^3 + b^3 = \frac{144}{8} = 18$$

I la solució és la D.

Els divisors de $2016$ són els productes de totes les diferents combinacions dels seus factors primers. Aquests factors primers són:

$$2016=2^5\cdot 3^2\cdot 7$$

És a dir, per construir un divisor, podem posar el $2$ multiplicant un cop, dos cops... fins a $5$ cops, i de manera equivalent amb el $3$ i el $7$. En total hi ha:

$$\text{n. divisors} = (5+1)\cdot (2+1)\cdot (1+1) = 6\cdot 3\cdot 2 = 36$$

Dels $36$ divisors, la meitat tindran un $7$ com a factor, i l'altra meitat no en tindran cap. El producte de tots els divisors tindrà $\frac{36}{2}=18$ sets, i per tant l'única solució que pot ser correcta és $2016^{18}$ i la solució és la D.

Si comptem el nombre de vegades que apareixen el $2$ i el $3$ en el producte de tots els divisors, veurem també que apareixen $18\cdot 5$ i $18\cdot 2$ vegades respectivament.

El residu sempre és més petit que el divisor, de manera que per obtindre els residus més grans possibles, hauríem de dividir pels divisors més grans possibles. En aquest cas, el divisor és la suma de les xifres d'un número més petit que $1000$.

El divisor més gran possible és $27$, amb el número $999$, però en aquest cas el residu és $0$:

$$999=27\cdot 37 + 0$$

El segon divisor més gran possible és $26$, amb els números $998, 989, 899$. Els residus són:

$$998 = 38\cdot 26 + 10$$ $$989 = 38\cdot 26 + 1$$ $$899 = 34\cdot 26 + 15$$

El tercer divisor més gran és $25$, que es correspon amb combinacions de $997$ i $988$. Quan dividim per $25$ és fàcil veure si el residu serà $24$: només cal fixar-se en les últimes dues xifres i veure si acaben en $24,49,74,99$. Per tant, podem veure que $799$ serà el nombre que ens donarà la resposta:

$$799 = 31\cdot 25 + 24$$

I la solució és la A.

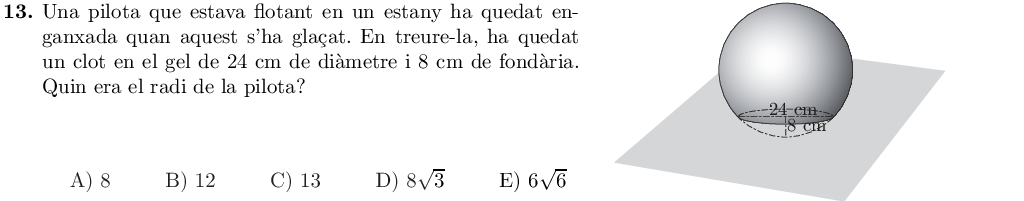
Podem fer un dibuix com el següent, que mostra una secció vertical de l'esfera:

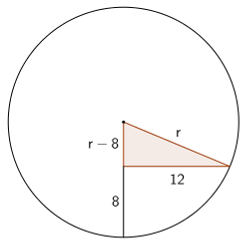
Veiem que tenim un triangle rectangle amb catets $12$ i $r-8$, i amb una hipotenusa $r$. Pel teorema de Pitàgores, tenim l'equació:

$$ \begin{array}{ccc} \\ \quad & 12^2 + (r-8)^2 = r^2 & \Rightarrow \\ \Rightarrow & 144 + r^2 - 16r +64 = r^2 & \Rightarrow \\ \Rightarrow & 208 - 16r = 0 & \Rightarrow \\ \Rightarrow & r=\frac{208}{16}=13 \end{array} $$

Per tant el radi mesura $13\text{ cm}$ i la solució és la C.

Al dau hi ha sis números: $1,2,3,4,5,6$. Adonem-nos que per tal que el producte de dos d'aquests números sigui més petit que la suma, un dels dos números ha de ser un $1$:

• Si un número és $1$, qualsevol que sigui l'altre, es complirà que $x+1 > 1\cdot x=x$.
• Si cap dels dos números és $1$, no es complirà mai. El cas que més s'apropa és quan surten dos $2$: $2+2 \ngtr 2\cdot 2$, i a partir d'aquí la diferència s'eixampla: $2+3 \ngtr 2\cdot 3$, $3+3 \ngtr 3\cdot 3$.

Així doncs, podem reformular l'enunciat com: quina és la probabilitat que surti algun número $1$ quan llancem els dos daus?

Per saber la probabilitat que surti algun $1$ hem de sumar la probabilitat que surti en el primer dau, més la probabilitat que surti en el segon, menys la probabilitat que surti en els dos (perquè és una possibilitat que hem comptat dos cops). El resultat és:

$$\frac16 + \frac16 - \frac16\cdot \frac16 = \frac{6 + 6 - 1}{36} = \frac{11}{36}$$

I la solució és la A.

En multiplicar l'alçada per un factor $x$, la proporció passa de $\frac23$ a $\frac{12}{5}$:

$$\frac23\cdot x = \frac{5}{12} \quad \Rightarrow \quad x = \frac{5}{12}\frac32 = \frac{15}{24} = \frac58$$

Per tant, hem retallat $1-\frac58 = \frac38$ de la fotografia. En tant per cent, és:

$$100\cdot \frac38 = 37,5\text{ \%}$$

I la solució és la C.

A l'equació $x^3+y^3 = x^2y^2$, crida l'atenció que a l'esquerra la $x$ i la $y$ estan elevades a $3$ i a la dreta estan elevades a $2$. Açò és significatiu perquè el resultat d'elevar un nombre negatiu al cub és negatiu, però és positiu si elevem el nombre al quadrat.

Per aquesta raó mai pot haver cap punt al quadrant $\text{III}$, ja que en aquest quadrant $x$ i $y$ són negatives, i per tant a l'esquerra de l'equació el valor és negatiu i a la dreta és positiu. Així doncs, la solució és la C.

Els radis i altures del cilindre petit i gran respectivament són:

$$r_1 = 15, \quad h_1 = 40, \quad r_2 = 20, \quad h_2 = 60$$

El volum total dels dos cilindres (el volum d'un cilindre és l'àrea del cercle de la base per l'altura) és:

$$V = V_1 + V_2 = \pi\cdot 15^2\cdot 40 + \pi\cdot 20^2\cdot 60 = 33.000\pi \text{ cm}^3$$

Sabem que en $3$ minuts el nivell ha pujat $5\text{ cm}$ (del cilindre petit), per tant, s'ompli al ritme:

$$\text{flux} = \frac{\pi\cdot 15^2\cdot 5}{3} = 375\pi \text{ cm}^3/\text{min}$$

Per omplir els dos dipòsits trigarà:

$$t=\frac{33000}{375} = 88\text{ min}$$

I la solució és la A.

Si descomposem un nombre en factors primers, aquest serà un quadrat perfecte si tots els exponents són parells, i serà un cub perfecte si tots els exponents són múltiples de $3$.

Pel que ens diu l'enunciat:

• $10A=2\cdot 5\cdot A$ és un quadrat perfecte. Llavors sabem que en la descomposició en factors primers d'$A$, el $2$ i el $5$ estan elevats a un exponent senar i qualsevol altre factor està elevat a un exponent parell.
• $6A=2\cdot 3\cdot A$ és un cub perfecte. Llavors sabem que en sumar $1$ als exponents de $2$ i $3$ en la descomposició d'$A$, els exponents són múltiples de $3$ i qualsevol altre factor està elevat a un exponent múltiple de $3$.

El nombre més petit que compleix aquestes propietats és:

$$A=2^5\cdot 3^2\cdot 5^3$$

El nombre de divisors d'un nombre és el producte dels exponents més $1$ de cada factor primer:

$$\text{n. divisors} = (5+1)\cdot (2+1)\cdot (3+1)= 6\cdot 3\cdot 4 = 72$$

La solució és la D.

Anomenem $x_1, x_2$ els costats del primer i el segon quadrat respectivament, i fixem arbitràriament el radi del cercle com a $1$. Llavors, podem fer la següent figura, observant els dos triangles rectangles que podem construir:

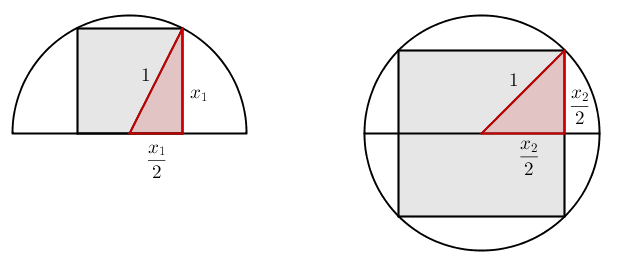
Pel Teorema de Pitàgores podem deduir:

$$x_1^2 + \left(\frac{x_1}2\right)^2 = 1^2 \quad \Rightarrow \quad \frac54x_1^2 = 1 \quad \Rightarrow \quad x_1 = \frac2{\sqrt5}$$ $$\left(\frac{x_2}2\right)^2 + \left(\frac{x_2}2\right)^2 = 1^2 \quad \Rightarrow \quad \frac{x_2^2}{2} = 1 \quad \Rightarrow \quad x_2 = \sqrt2$$

Les àrees dels quadrats, per tant, són:

$$x_1^2 = \frac45, \quad x_2^2 = 2$$

Com la primera placa quadrada pesa $2$ grams, la segona pesa:

$$\frac2{\frac45}\cdot 2 = 5\text{ grams}$$

I la solució és la D.

En primer lloc, podem trobar una solució trivial amb $x=1, y=6$:

$$1!\cdot 7! = (1+6)!$$

Per tal que $x\cdot 7!$ sigui en si un factorial, podem fer que $x=7!-1$, i llavors, amb $y=1$:

$$(7!-1)!\cdot 7! = (7!)! = ((7!-1) + 1)!$$

Una altra manera de resoldre l'equació seria si poguéssim trobar una $x$ de la forma $x=8\cdot 9\cdot 10\cdots$. No cal provar molt per adonar-nos que: $8\cdot 9\cdot 10 = 720 = 6!$, per tant, amb $x=6, y=4$:

$$7!\cdot 6! = 10! = (6+4)!$$

En total, hem trobat $3$ solucions per a l'equació, falta veure si poden haver-hi infinites.

Però no poden haver infintes solucions perquè amb $x>7!$, $x!\cdot 7!$ mai pot ser un factorial, i per tant el nombre de solucions ha de ser per força finit.

Així, la solució és la E.

Resoldrem aquest problema usant el Petit teorema de Fermat, que diu:

«Si $p$ és un nombre primer, aleshores, per cada nombre natural $a$ coprimer amb $p$, $a^{p-1} \equiv 1 (\text{mod } p)$»

L'equació $a^{p-1} \equiv 1 (\text{mod } p)$ es llegeix «$a$ elevat a $p$ menys $1$ és congruent amb $1$ mòdul $p$», i vol dir que en dividir $a^{p-1}$ per $p$, el residu de la divisió és $1$.

Podem aplicar aquest teorema al nostre problema amb $p=3$ (la $p$ del teorema), llavors tenim que:

$$p^2 \equiv 1 (\text{mod } 3) \quad \Rightarrow \quad p^2 + 2 \equiv 3 (\text{mod } 3) \equiv 0 (\text{mod } 3)$$

Així hem vist que per qualsevol $p$ que siga coprimer amb $3$, $p^2 + 2$ serà un múltiple de $3$, i per tant no pot ser primer.

Tots els nombres primers són coprimers amb $3$ excepte el $3$ mateix. Per $3$:

$$3^2+2=11 \text{( primer)}$$

De manera que només pot haver un nombre $p$ que compleixi que $p^2+2$ és també primer, i la solució és la B.

En primer lloc, comptem de quantes maneres diferents podem triar $3$ punts entre els $12$ punts que hi ha, sense importar l'ordre. La resposta és:

$$ \begin{pmatrix} 3 \\ 12 \end{pmatrix} = \frac{12\cdot 11\cdot 10}{3\cdot 2} = 220 $$

Però no totes aquestes combinacions formen triangles, perquè pot ser que els tres punts estiguen alineats. Comptem les maneres que tenim de triar $3$ punts sobre un mateix costat:

$$ \begin{pmatrix} 3 \\ 5 \end{pmatrix} = \frac{5\cdot 4\cdot 3}{3\cdot 2} = 10 $$

Com hi ha $3$ costats, en total hi ha $3\cdot 10=30$ formes diferents de triar $3$ punts alineats.

En total es poden dibuixar $220-30=190$ triangles diferents i la solució és la E.

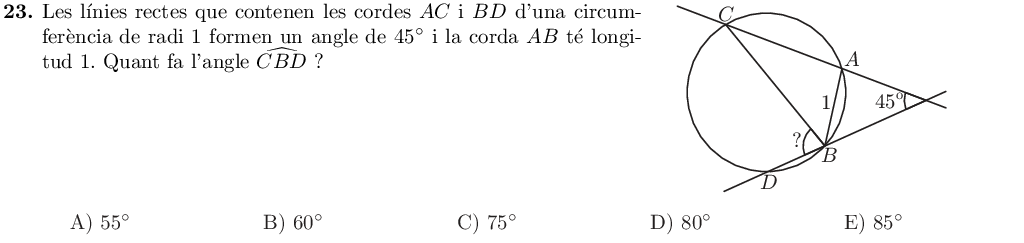
A continuació fem un dibuix sobre el que raonarem:

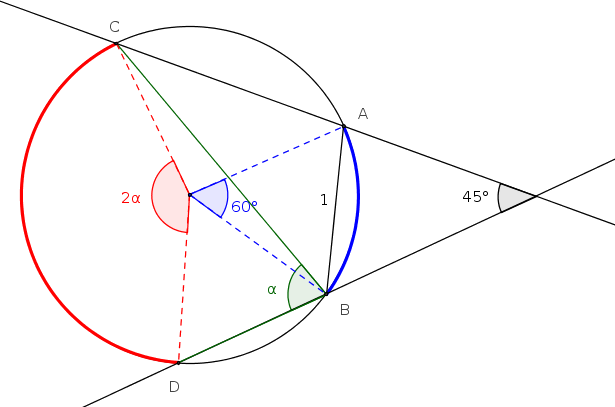
L'angle que volem esbrinar, $\alpha$ (verd), és un angle inscrit a la circumferència, i per tant abarca un arc que mesura el doble, $\stackrel{\textstyle\frown}{\mathrm{CD}} = 2\alpha$ (vermell).

Per altra banda, coneixem la mesura de l'arc blau, que és $\stackrel{\textstyle\frown}{\mathrm{AB}} = 60^\circ$ perquè la corda $\overline{AB}$ mesura $1$, igual que el radi, i per tant formen un triangle equilàter.

Per acabar, el Teorema de l'angle exterior diu que l'angle que formen dues rectes secants amb una circumferència ($45^\circ$ en el nostre cas), és la meitat de l'arc gran menys el petit:

$$ 45 = \frac{\stackrel{\textstyle\frown}{\mathrm{CD}} - \stackrel{\textstyle\frown}{\mathrm{AB}}}{2} \quad \Rightarrow \quad 45 = \frac{2\alpha - 60}{2} \quad \Rightarrow \quad \alpha = 75^\circ $$

I per tant la solució és la C.

Si volem pintar un edifici de $10$ plantes, per començar tenim dues opcions: pintar la primera planta de blau o pintar-la de groc:

• Si pintem la primera planta de blau, per força la segona planta la pintarem de groc. A partir d'aquí, podem pintar les $8$ plantes restants com volguem.
• Si pintem la primera planta de groc, podrem pintar les $9$ plantes restants com volguem.

Si anomenem $N_{10}$ el nombre de formes distintes de pintar les $10$ plantes sense pintar-ne dues consecutives de blau, el que hem vist és que:

$$N_{10} = N_8 + N_9$$

Amb $N_8$ i $N_9$ tindrem la mateixa propietat, que és que cada nombre de la successió és la suma dels dos anteriors (i que no és altra que la Successió de Fibonacci):

$$N_n = N_{n-1} + N_{n-2}$$

Per esbrinar el valor de $N_{10}$ començarem amb els casos més senzills:

• $N_1=2$: podem pintar una planta de dues formes, o de blau o de groc.
• $N_2=3$: podem pintar dues plantes de tres formes: (blau, groc), (groc, blau) i (groc, groc).

A partir d'aquí, cada element és la suma dels dos anteriors, per tant tenim la successió:

$$N_1=2, \quad N_2=3, \quad N_3=5,$$ $$N_4=8, \quad N_5=13, \quad N_6=21,$$ $$N_7=34, \quad N_8=55, \quad N_9=89,$$ $$N_{10}=144$$

I la solució és la D.

Els costats dels triangles han de mesurar: $1,2,3,4,5\text{ o }6$. Per tal de poder formar un triangle, tres segments han de complir el que s'anomena desigualtat triangular, que diu que un segment no pot ser tant o més llarg que la suma dels altres dos. Per exemple, els segments $(6,3,3)$ no poden formar un triangle.

Comptarem el nombre de triangles buscant terns $(a,b,c)$ amb $a\geq b\geq c$. Com $a,b,c$ estan ordenats de major a menor, la desigualtat triangular es complirà si $b+c > a$, o dit d'una altra manera, $c > a-b$.

Per cada parella de valors $(a,b)$, comptarem quants valors pot prendre $c$ de manera que es compleixi la desigualtat anterior $(c > a-b)$, i també que sigui menor o igual que $b$, és a dir:

$$b \geq c > a-b$$

Per exemple

• Si tenim $(6,6)$, s'ha de complir $6 \geq c > 6-6=0$, i per tant $c$ pot prendre $6$ valors: $1,\ldots,6$.
• Si tenim $(4,3)$, s'ha de complir $3 \geq c > 4-3=1$, i per tant $c$ pot prendre $2$ valors: $2,3$.

I així calculem el nombre de possibilitats:

$$ \begin{array}{cccccc} (6,6)\rightarrow6 & (5,5)\rightarrow5 & (4,4)\rightarrow4 & (3,3)\rightarrow3 & (2,2)\rightarrow2 & (1,1)\rightarrow1 \\ (6,5)\rightarrow4 & (5,4)\rightarrow3 & (4,3)\rightarrow2 & (3,2)\rightarrow1 \\ (6,4)\rightarrow2 & (5,3)\rightarrow1 \end{array} $$

En total:

$$6+4+5+3+1+2+4+2+3+1+2+1 = 34$$

Hi ha $34$ triangles diferents que es poden fer i la solució és la E.

Anomenem $x$ la despesa anual que es fa de petroli, de manera que hi ha una reserva total de $50x$. Cada any es reduirà la despesa de manera proporcional i anomenem $r$ aquesta proporció. Llavors, la despesa total de petroli seguirà una progressió geomètrica. La suma infinita de la progressió serà la quantitat total de petroli que hi ha, és a dir, caldrà una eternitat per gastar tota la reserva de petroli:

$$\sum^{\infty}_{n=0}xr^n = 50x$$

Es tracta d'una progressió geomètrica infinita la suma de la qual és $\frac{x}{1-r}$. Podem plantejar l'equació:

$$\frac{x}{1-r} = 50x \quad \Rightarrow \quad 1= 50\cdot (1-r) = 50 - 50r \quad \Rightarrow \quad r = \frac{49}{50}$$

Una proporció de $\frac{49}{50}$ en tant per cent és $100\cdot \frac{49}{50}=98\%$. Si s'utilitza un $98\%$ del petroli de l'any anterior, significa que s'ha reduit el consum en un $2\%$ i per tant la solució és la B.

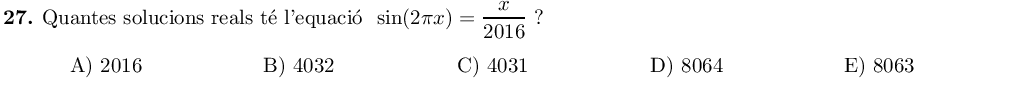
En primer lloc, adonem-nos que a l'esquerra de l'equació tenim un sinus, de manera que el seu valor estarà a l'interval $[-1, 1]$. Per tal de no sobrepassar aquest límit a la dreta de l'equació, la $x$ haurà d'estar a l'interval $[-2016, 2016]$.

Per comptar el nombre de solucions dibuixarem la gràfica de les dues funcions, i comptant el nombre d'interseccions sabrem el nombre de solucions. Les gràfiques són:

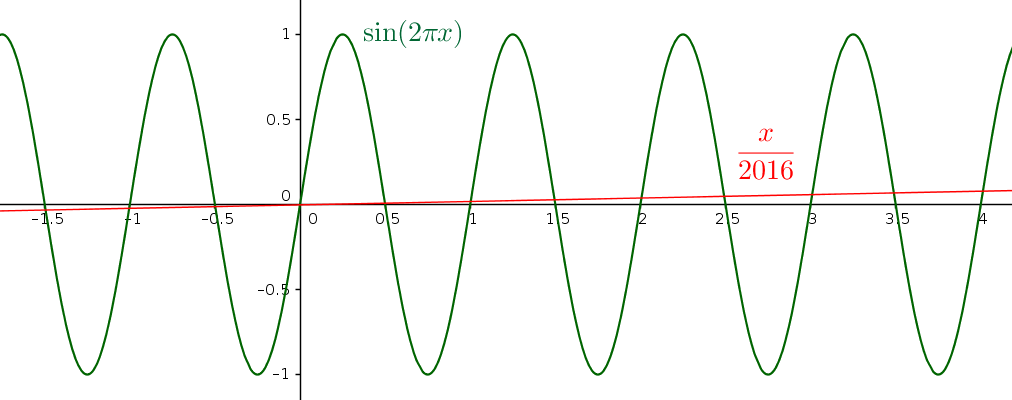
Per la banda positiva, la recta talla el sinus dos cops per cada turó, i els turons estan situats als intervals $(n, n+0.5)$. Concretament, les gràfiques es tallaran $2$ cops a cada interval $(0,0.5), (1, 1.5), \ldots, (2015, 2015.5)$. En total, es tracta de $2\cdot 2016$ interseccions.

Per la banda negativa, el raonament és el mateix, de manera que hi ha també $2\cdot 2016$ interseccions.

Ara bé, hem comptat dos cops una mateixa intersecció: la de l'origen de coordenades $(x=0)$. Així doncs, el nombre total de solucions és:

$$2\cdot 2016+2\cdot 2016-1=8063$$

I la solució és la E.

Podem expressar la primera equació com:

$$f(xy) = \frac{f(x)}y$$

Llavors, podem buscar $f(24)$ amb:

$$f(24) = f(8\cdot 3) = \frac{f(8)}3$$

I podem esbrinar el valor de $f(8)$ amb:

$$f(32) = f(8\cdot 4) = \frac{f(8)}4 = 63 \quad \Rightarrow \quad f(8) = 63\cdot 4 = 252$$

Finalment:

$$f(24) = \frac{f(8)}3 = \frac{252}3 = 84$$

I la solució és la D.

Anomenem $\beta$ l'angle que volem esbrinar, i anomenem $\alpha, \alpha'$ els dos angles aguts del triangle rectangle $AFG$. Com és un triangle rectangle, aquests dos angles són complementaris, és a dir, $\alpha+\alpha'=90^\circ$.

Ara projectem el punt $D$ als dos altres costats, i anomenem $D_1, D_2$ els nous punts. Tal com es veu a la figura, tenim dos triangles rectangles ($ADD_1, DD_2C$, en vermell clar) que tenen els mateixos angles, i a més, la seua hipotenusa mesura el mateix (les hipotenuses són costats del quadrat). Per tant, els triangles vermells són iguals.

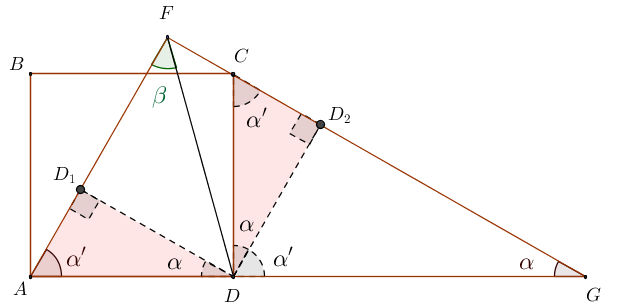
Com els triangles $ADD_1$ i $DD_2C$ són iguals, el quadrilàter $DD_2FD_1$ és un quadrat, i el segment $FD$ és una diagonal del quadrat. Llavors, l'angle $\beta$ que volíem esbrinar és la meitat de l'angle recte i per tant mesura $45^\circ$.

La solució és la C.

Descartem en primer lloc que aquest matemàtic nasqués abans de $1900$. Si fós així, el $1955$ tindria més de $55$ anys, però de cap manera podem obtindre $55$ com a suma de $4$ xifres.

Vist que va nàixer després de $1900$, anomenem $19XY = 1900 + 10X + Y$ el seu any de naixement. Fixem-nos que:

• L'edat d'una persona és la resta entre l'any actual i l'any de naixement, de manera que el $1955$ té $1955 - (1900 +10X + Y) = 55 - 10X - Y$ anys.
• L'enunciat ens diu que la seua edat és la suma de les xifres de l'any de naixement: $1+9+X+Y=10+X+Y$.

Per tant, tenim:

$$10+X+Y = 55 - 10X - Y \quad \Rightarrow \quad 11X + 2Y = 45$$

L'única solució entera amb $X,Y<10$ d'aquesta equació és $X=3, Y=6$. Per tant el matemàtic va nàixer l'any $1936$, va fer $50$ anys el $1986$ i la suma de les xifres d'aquest any és $1+9+8+6=24$.

La solució és la D.

Aquest famós matemàtic bé podria ser Miguel de Guzmán, matemàtic murcià que entre altres coses va ser un gran divulgador i fundador del projecte ESTALMAT.