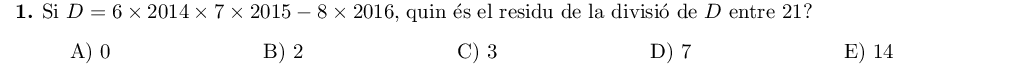
Intentarem simplificar la divisió eliminant els termes que siguen múltiples de $21$, ja que per aquests el residu serà zero. Com que $21=3\cdot 7$, els múltiples de $21$ tindran $3$ i $7$ entre els seus factors primers. Fixem-nos en cada terme de la resta:

• $6\times2014\times7\times2015$ conté el factor $7$ i també el $3$ (perquè $6=2\cdot 3$), per tant és múltiple de $21$.
• Podem expressar $8\cdot 2016$ com $8\cdot 2^5\cdot 3^2\cdot 7$ si factoritzem $2016$, i per tant veiem que també és un múltiple de $21$.

La resta de dos múltiples de $21$ serà múltiple de $21$ i per tant el residu és $0$. La solució és la A.

Anomenem $h$ l'altura de cada franja, de manera que l'altura del triangle és $5h$. De manera anàloga, anomenem $b$ la base del petit triangle superior, de manera que la resta de franges tenen una base de $2b, 3b, 4b$ i el triangle gran té una base $5b$ (pel Teorema de Tales). Podem calcular la proporció grisa amb:

$$\frac{A_{gris}}{A_{total}} = \frac{A_{triangle\ petit} + A_{trapezi_1} + A_{trapezi_2}}{A_{triangle\ gran}}$$

Calculem ara l'àrea de cadascuna d'aquestes figures, recordant que l'àrea d'un trapezi és la meitat de l'altura per la suma de les bases:

$$A_{triangle\ gran}=\frac12\cdot 5b\cdot 5h = \frac{25}2bh$$

$$A_{triangle\ petit} = \frac12bh$$

$$A_{trapezi_1} = \frac12\cdot (2+3)b\cdot h = \frac52bh$$

$$A_{trapezi_2} = \frac12\cdot (5+4)b\cdot h = \frac92bh$$

I ara fem la divisió:

$$\frac{A_{gris}}{A_{total}} = \frac{\frac12bh+\frac52bh+\frac92bh}{\frac{25}2bh}= \frac{1+5+9}{25}=\frac{15}{25}=\frac{60}{100} = 60\%$$

I la solució és la A.

La única figura que no cap és la E. Per tal de tenir una àrea igual a la del quadrat, el triangle equilàter haurà de sobresortir, com veiem a la figura:

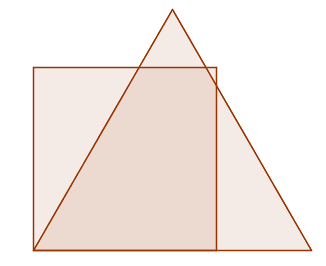
La resta d'opcions caben dins del quadrat:

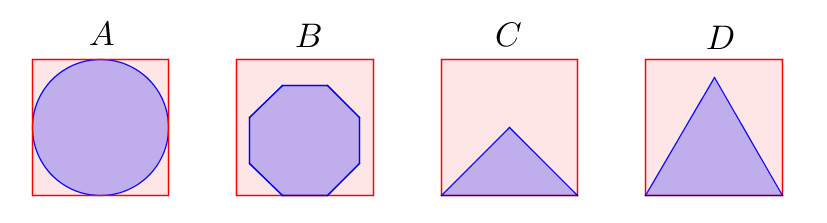
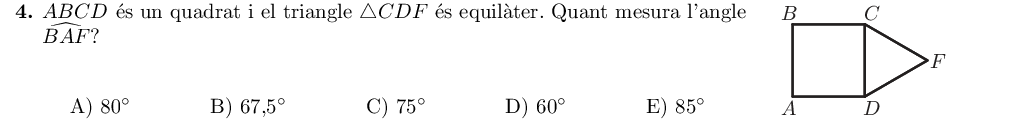
Els costats del quadrat i del triangle mesuren el mateix, ja que comparteixen el costat $CD$. Així, el triangle $ADF$ és isòsceles. Centrant-nos en aquest triangle, podem dibuixar la figura:

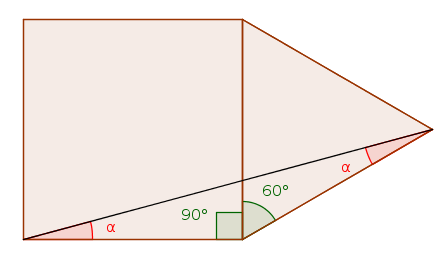
Com coneixem els angles del quadrat i del triangle, podem esbrinar l'angle $\alpha$:

$$\alpha = \frac{180 - (90+60)}2 = \frac{30}2=15$$

Per tant, l'angle $BAF$ serà l'angle recte menys l'angle $\alpha$: $90-15=75$; i la solució és la C.

La línia poligonal sempre comença a la lletra $K$, però llavors pot anar a qualsevol de les dues lletres $A$, així que de moment tenim $2$ opcions. La línia continuarà amb les lletres $N,G,A,R$ (només queda una $A$), i finalment pot passar per qualsevol de les dues $O$, per acabar a l'altra $O$, és a dir, hi ha $2$ possibilitats més.

En total, hi ha $2\cdot 2=4$ línies diferents i la solució és la D.

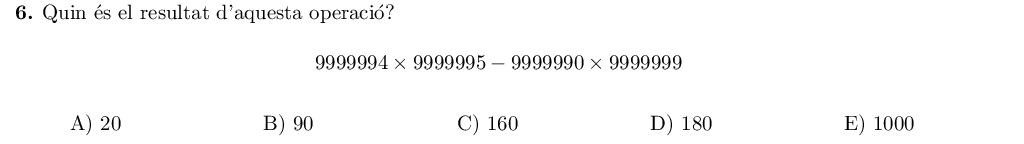
Simplificarem els càlculs usant $x=9999990$, llavors:

$$9999994\times9999994 - 9999990\times9999999 =$$ $$(9999990+4)\cdot (9999990+4) - 9999990\cdot (9999990 + 9) =$$ $$(x + 4)\cdot (x+5) - x\cdot (x+9) =$$ $$x^2 + 4x + 5x + 20 - x^2 - 9x = 20$$

I la solució és la A.

Inicialment, $\frac13$ compraven $B$. A aquests cal sumar-lost $\frac14$ dels que compraven $A$, que eren $\frac23$:

$$\frac13 + \frac14\cdot \frac23 = \frac13 + \frac2{12} = \frac4{12} + \frac2{12} = \frac{6}{12} = \frac12$$

La solució és la D.

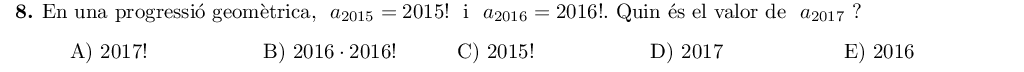
En una progressió geomètrica, cada terme és igual al terme anterior multiplicat per un nombre (anomenat raó). Per passar de $a_{2015}=2015!$ a $a_{2016}=2016!$, hem multiplicat per $2016$. Per obtindre $a_{2017}$, hem de multiplicar també per $2016$: $a_{2017}=2016\cdot 2016!$, i la solció és la B.

Si $\frac1N$ es pot escriure com un decimal exacte, vol dir que per a un cert nombre de zeros, $10\ldots0$ és divisible per $N$. Els nombres $10\ldots0$, que són múltiples de $10$, tenen una factorització $2^n\cdot 5^n$, on $n$ és el nombre de xifres.

Per tal que $N$ siga divisor de $2^n\cdot 5^n$, cal que $N$ només tinga el $2$ i el $5$ en la seua descomposició en factors primers. Si provem les opcions que ens donen, és evident que $96$ té el $3$ com a factor primer, però en canvi, $80=2^4\cdot 5$.

Per tant, la solució és $80$, la D. Efectivament:

$$\frac1{80}=0,0125$$

Anomenem $n$ el nombre de membres de la penya. Quan es reparteixen en $24$ minibusos enlloc de'n $32$, hi ha $2$ persones més per minibus, llavors:

$$\frac{n}{32} + 2=\frac{n}{24} \quad \Rightarrow \quad \frac{n}{24}-\frac{n}{32}=2 \quad \Rightarrow \quad $$ $$ \frac{4n}{96} - \frac{3n}{96} = 2 \quad \Rightarrow \quad \frac{n}{96} = 2 \quad \Rightarrow \quad $$ $$ n = 96\cdot 2=192 $$

La solució és la C.

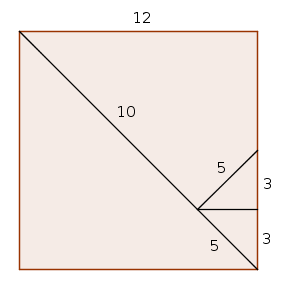
L'àrea del rectangle és $16\cdot 9=144$, de manera que si formem un quadrat d'aquesta àrea, el costat serà $\sqrt{144}=12$ i per tant el seu perímetre serà $4\cdot 12=48$, l'opció C. Comprovem que podem formar aquest quadrat:

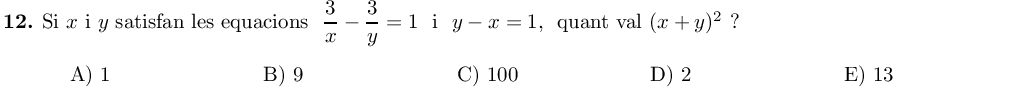
En primer lloc operem amb $(x+y)^2$:

$$(x+y)^2 = x^2 + 2xy + y^2 = x^2 - 2xy + y^2 + 4xy = (y-x)^2 + 4xy$$

Per la segona equació de l'enunciat sabem que $y-x=1$, per tant:

$$(x+y)^2 = 1^2 + 4xy$$

Ara, començant amb la primera equació de l'enunciat:

$$\frac3x - \frac3y = 1 \quad \Rightarrow \quad \frac{3y-3x}{xy} = 1 \quad \Rightarrow \quad 3y-3x = xy$$

Com que $y-x=1$, tenim que:

$$xy = 3y-3x = 3(y-x) = 3$$

Llavors, com volíem saber:

$$(x+y)^2 = 1 + 4xy = 1 + 4\cdot 3 = 13$$

I la solució és la E.

En primer lloc comptem de quantes maneres podem col·locar les lletres $U$. A la primera fila va una lletra $U$, a una de les $3$ caselles. La segona $U$ va a la segona fila, però només pot anar a una de dues caselles (no pot estar a la mateixa columna que la primera lletra $U$). Per tant, hi ha:

$$3\cdot2=6$$

formes de col·locar les lletres $U$.

La resta de lletres de $SUDOKU$, és a dir, $S,D,K,O$ són diferents. Les haurem de situar a les quatre caselles lliures. Hi ha tantes maneres diferents de fer-ho com permutations de les lletres $SDKO$, és a dir, $4!$. En total, hi ha:

$$6\cdot 4!=6\cdot 24=144$$

formes d'escriure $SUDOKU$ tal com demana l'enunciat, i la solució és la E.

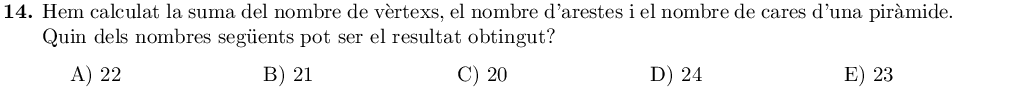
Els vèrtexs, arestes i cares d'una piràmide vindran donats pel nombre de vèrtexs que té el polígon de la base. Si la base de la piràmide és un polígon de $n$ vèrtexs, la piràmide té:

• $n+1$ vèrtexs: els de la base més la cúspide.
• $2n$ arestes: $n$ arestes al polígon de la base i $n$ arestes que van de de cada vèrtex a la cúspide.
• $n+1$ cares: la base més una cara formada per cada aresta de la base i la cúspide.

Així, la suma de vèrtexs, arestes i cares és:

$$(n+1) + 2n + (n+1) = 4n+2$$

De les opcions que se'ns presenten, només una es correspon a aquesta forma: $22=4\cdot 5 + 2$ (ho podem comprovar dividint cada opció per $4$ i veient que el residu només és $2$ per a $22$). La solució és la E.

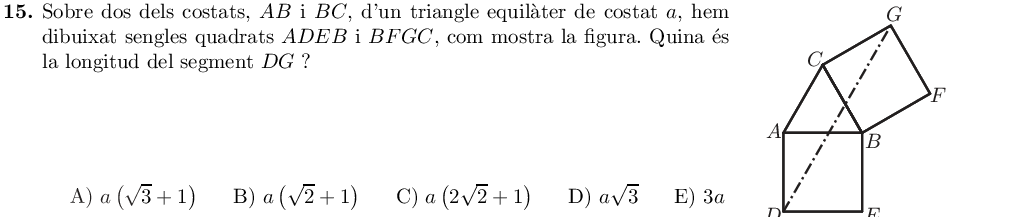
Girem la figura i anomenem $x$ el segment del qual volem saber la longitud, i $y$ el segment que completa $a$ per formar un triangle a sota.

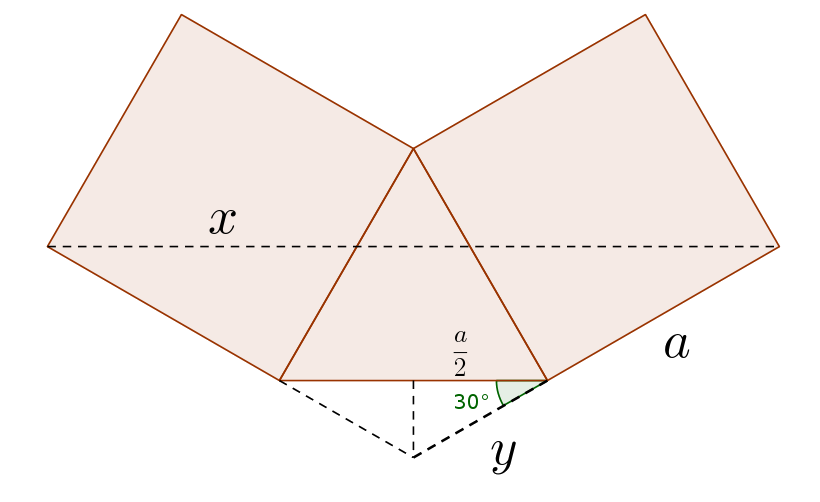
Pel Teorema de Tales sabem que:

$$\frac{y}{y+a} = \frac{a}{x} \quad \Rightarrow \quad x=\frac{a(y+a)}y$$

Mitjançant el triangle rectangle que hem dibuixat i que té un angle de trenta graus, podem esbrinar el valor de $y$:

$$\cos30^\circ = \frac{\sqrt3}2 = \frac{\frac{a}2}y \quad \Rightarrow \quad y = \frac{a}{\sqrt3}$$

I llavors podem trobar $x$:

$$x = \frac{a\left(\frac{a}{\sqrt3}+a\right)}{\frac{a}{\sqrt3}} = \frac{\frac{a + \sqrt3a}{\sqrt3}}{\frac1{\sqrt3}}=a\left(1+\sqrt3\right)$$

I la solució és la D.

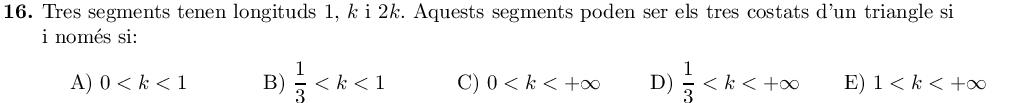
Els tres segments han de complir la desigualtat triangular, que diu que la longitud d'un segment no pot ser major que la suma dels altres dos.

Per una banda, comprovem que els costats $k$ i $2k$ sumen una longitud major que $1$:

$$1 <k + 2k \quad \Rightarrow \quad \frac13 < k$$

Per una altra banda, els segments $1$ i $k$ han de sumar una longitud major que $2k$:

$$2k < 1+k\quad \Rightarrow \quad k < 1$$

En resum, tenim que:

$$\frac13 < k < 1$$

I la solució és la B.

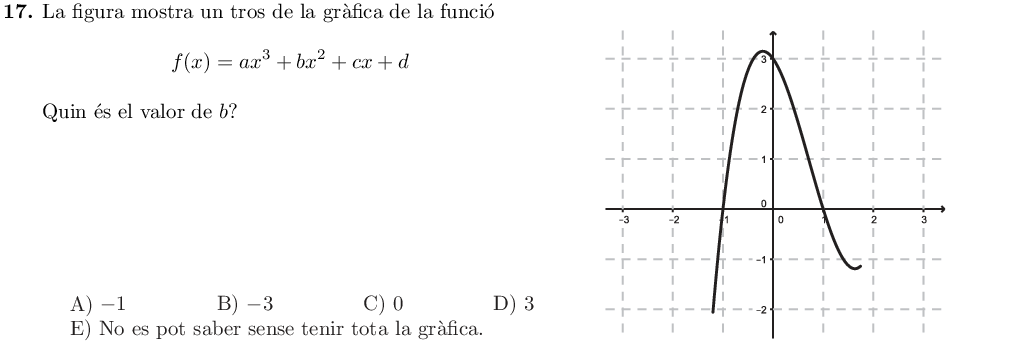
A la figura veiem que la gràfica passa pels punts:

$$(x, y) = \left\\{(-1,0),\; (0,3),\; (1, 0)\right\}$$

Usant aquesta informació, buscarem el valor de $b$.

Pel segon punt sabem que:

$$a\cdot 0^3+b\cdot 0^2+c\cdot 0+d=3 \quad \Rightarrow \quad d = 3$$

Pel primer i tercer punts tenim el sistema:

$$\begin{cases} -&a &+& b &-& c &+& d & = & 0\\ &a &+& b &+& c &+& d & = & 0 \end{cases}$$

Sumant les dues equacions tenim:

$$2b+2d =0 \quad \Rightarrow \quad b = -d = -3$$

I la solució és la B.

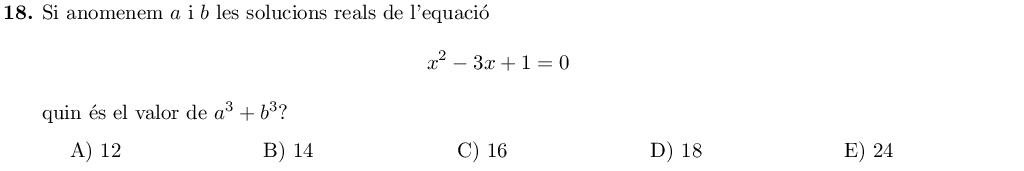
Comencem resolent el sistema:

$$x = \frac{3 \pm \sqrt{3^2-4}}{2} = \frac{3 \pm \sqrt5}{2}$$ $$a = \frac{3 + \sqrt5}{2}, \quad b = \frac{3 - \sqrt5}{2}$$

LLavors, tenim que:

$$a^3+b^3 = \left(\frac{3 + \sqrt5}{2}\right)^3 + \left(\frac{3 - \sqrt5}{2}\right)^3 =$$ $$= \frac{(3+\sqrt5)^3 + (3-\sqrt5)^3}{8}$$

Per fer la suma $(3+\sqrt5)^3 + (3-\sqrt5)^3$, tinguem en compte que:

$$(a+b)^3 = a^3 + 3a^2b + 3ab^2 + b^3$$ $$(a-b)^3 = a^3 - 3a^2b + 3ab^2 - b^3$$

I la suma és:

$$(a+b)^3 + (a-b)^3 = 2a^3 + 6ab^2$$

Per tant:

$$(3+\sqrt5)^3 + (3-\sqrt5)^3 = 2\cdot 3^3 + 6\cdot 3\cdot \sqrt{5}^2 =$$ $$= 54 + 18\cdot 5 = 144$$

En definitiva, tenim que:

$$a^3 + b^3 = \frac{144}{8} = 18$$

I la solució és la D.

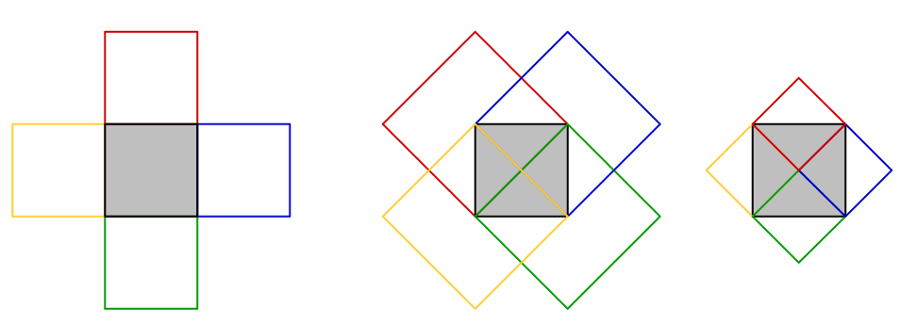
En total hi ha $12$ quadrats diferents, com podem veure a la figura següent, i la solució és la E.

En primer lloc fixem-nos que tots els nombres primers són senars excepte un: el $2$.

Albert escriu una quantitat parella de nombres primers, i la suma és senar. Si tots els nombres primers que ha escrit fóssin senars, la suma seria parella, de manera que entre els nombres que ha escrit hi és el $2$.

Blanca ha escrit una quantitat senar de nombres primers, i la suma és parella. Si només hagués escrit nombres primers senars, la suma seria senar, de manera que ha d'haver escrit el número $2$.

De manera que tant per l'Albert com per la Blanca, els productes de nombres contenen el $2$ i per tant el resultat és parell. La solució és la C.

Per una errada en l'enunciat, l'opció A és equivalent a l'opció C, de manera que aquesta també és una solució correcta.

A l'equació $x^3+y^3 = x^2y^2$, crida l'atenció que a l'esquerra la $x$ i la $y$ estan elevades a $3$ i a la dreta estan elevades a $2$. Açò és significatiu perquè el resultat d'elevar un nombre negatiu al cub és negatiu, però és positiu si elevem el nombre al quadrat.

Per aquesta raó mai pot haver cap punt al quadrant $\text{III}$, ja que en aquest quadrant $x$ i $y$ són negatives, i per tant a l'esquerra de l'equació el valor és negatiu i a la dreta és positiu. Així doncs, la solució és la D.

Si anomenem $x$ la llargada de les espelmes, aquestes cremen al ritme:

$$\frac{x}{5},\quad \frac{x}{4}$$

Després d'un temps $t$, queda la següent llargada per cada espelma:

$$x-t\frac{x}{5} = \frac{x}5(5-t),\quad x-t\frac{x}{4} = \frac{x}4(4-t)$$

Com una és quatre vegades més llarga que l'altra, tenim que:

$$\frac{\frac{x}5(5-t)}{\frac{x}4(4-t)} = 4 \quad \Rightarrow$$ $$\Rightarrow \quad \frac{4\cdot (5-t)}{5\cdot (4-t)} = \frac{20 - 4t}{20 -5t}=4 \quad \Rightarrow$$ $$\Rightarrow \quad 20-4t = 80-20t \quad \Rightarrow$$ $$\Rightarrow \quad 16t=60\quad \Rightarrow \quad t=3+\frac34$$

És a dir, han passat $3$ hores i $3$ quarts, i per tant són les 22.45. La solució és la B.

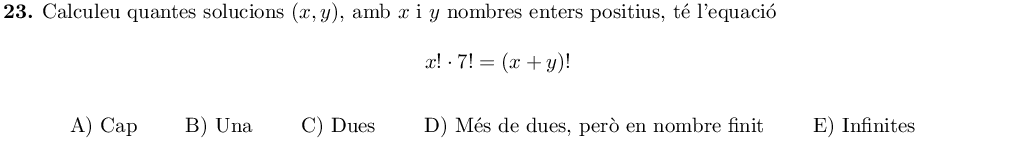
En primer lloc, podem trobar una solució trivial amb $x=1, y=6$:

$$1!\cdot 7! = (1+6)!$$

Per tal que $x\cdot 7!$ sigui en si un factorial, podem fer que $x=7!-1$, i llavors, amb $y=1$:

$$(7!-1)\cdot 7! = (7!)! = ((7!-1) + 1)!$$

Una altra manera de resoldre l'equació seria si poguéssim trobar una $x$ de la forma $x=8\cdot 9\cdot 10\cdots$. No cal provar molt per adonar-nos que: $8\cdot 9\cdot 10 = 720 = 6!$, per tant, amb $x=6, y=4$:

$$7!\cdot 6! = 10! = (6+4)!$$

En total, hem trobat $3$ solucions per a l'equació, falta veure si poden haver-hi infinites.

Però no poden haver infintes solucions perquè amb $x>7!$, $x!\cdot 7!$ mai pot ser un factorial, i per tant el nombre de solucions ha de ser per força finit.

Així, la solució és la D.

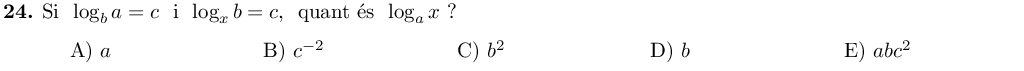
Expressem el que signifiquen els logaritmes de l'enunciat, i anomenem $?$ el que volem esbrinar:

$$b^c=a, \quad x^c=b, \quad a^?=x$$

Llavors podem veure que:

$$b^c=a \quad \Rightarrow \quad b=a^{\frac1c}$$ $$x^c=b=a^{\frac1c} \quad \Rightarrow \quad x=a^{\frac1{c^2}}=a^{c^{-2}}$$

I la solució és $c^{-2}$, la B.

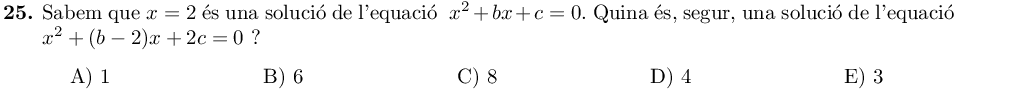
Si $x=2$ és solució de $x^2+bx+c=0$, llavors:

$$2^2+2b+c=0 \quad \Rightarrow \quad c = -2b -4$$

Podem expressar la segona equació com:

$$x^2 + (b-2)x + 2(-2b-4) = 0 \quad \Rightarrow \quad$$ $$\Rightarrow \quad x^2 + bx - 2x - 4b -8 = 0 \quad \Rightarrow \quad$$ $$\Rightarrow \quad b(x-4) + x^2 - 2x -8 = 0\quad\quad\quad$$

Comprovem que amb $x=4$ s'elimina el terme amb la $b$ i la resta també val $0$:

$$b(4-4) + 4^2 - 2\cdot 4 -8 = 0$$

I la solució és la D.

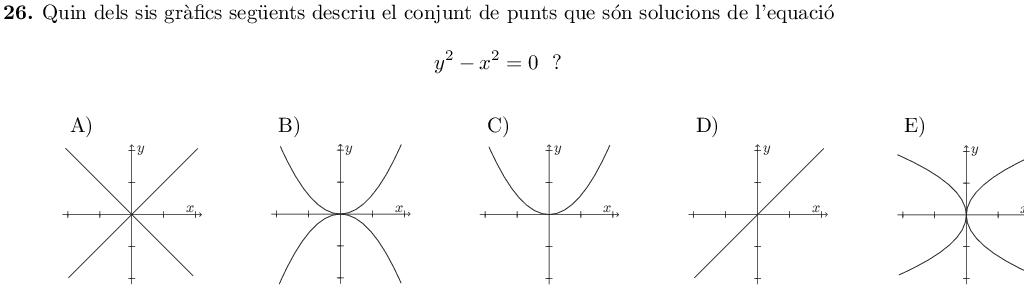
Podem escriure l'equació com $y^2=x^2$. Per cada nombre positiu $a$, seran solucions de l'equació $\left\{(a,a), (-a, a), (a, -a), (-a, -a)\right\}$. Aquestes solucions es corresponen amb la gràfica A.

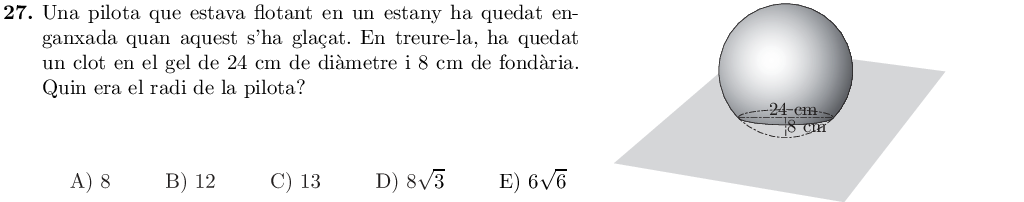
Podem fer un dibuix com el següent, que mostra una secció vertical de l'esfera:

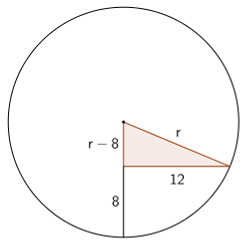
Veiem que tenim un triangle rectangle amb catets $12$ i $r-8$, i amb una hipotenusa $r$. Pel teorema de Pitàgores, tenim l'equació:

$$ \begin{array}{ccc} \\ \quad & 12^2 + (r-8)^2 = r^2 & \Rightarrow \\ \Rightarrow & 144 + r^2 - 16r +64 = r^2 & \Rightarrow \\ \Rightarrow & 208 - 16r = 0 & \Rightarrow \\ \Rightarrow & r=\frac{208}{16}=13 \end{array} $$

Per tant el radi mesura $13\text{ cm}$ i la solució és la C.

Solució alternativa proposada per Gabriel als comentaris

Cadascuna de les dues parelles de triangles de bases oposades té una àrea de mig quadrat. Si anomenem $h$ l'altura d'un dels triangles, l'altura del triangle oposat serà $x-h$, llavors la suma de les àrees és:

$$x\cdot\frac{h}2 + x\cdot\frac{x-h}2 = x\cdot\frac{h+x-h}2 = \frac{x^2}2$$

És a dir, la meitat de l'àrea del quadrat.

Si anomenem $x$ l'àrea del triangle que no coneixem, hi ha tres opcions:

$$ \begin{array}{ccccc} 20+2=16+x & \quad\Rightarrow\quad & x=6 & & \\ 16+2=20+x & \quad\Rightarrow\quad & x=-2 & \rightarrow & \text{No pot ser} \\ 20+16=2+x & \quad\Rightarrow\quad & x=34 & \rightarrow & \text{No està a les opcions} \end{array} $$

Llavors la solució ha de ser $x=6$, l'opció B.

Solució original

Anomenem $x$ el costat del quadrat, i $a,b$ la distància del punt de dins del quadrat al costat inferior i esquerre respectivament. Llavors, els quatre triangles tenen una base $x$ i unes altures $a, b, x-a, x-b$, tal com es veu a la figura:

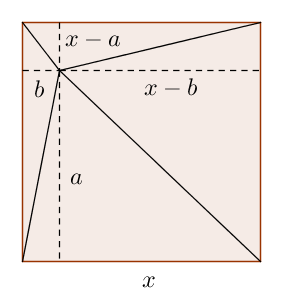
Decidim arbitràriament que $a$ és l'altura més gran, i per tant, forma el triangle d'àrea més gran:

$$20=\frac12\cdot x\cdot a \quad \Rightarrow \quad a=\frac{40}x$$

Dels dos altres triangles amb àrea coneguda ($16$ i $2$), podem suposar que el d'àrea $16$ té una altura $b$, per tant:

$$16=\frac12\cdot x\cdot a \quad \Rightarrow \quad b=\frac{32}x$$

Ara hi ha dues possibilitats: que el triangle d'àrea $2$ tingui altura $x-a$ o que tingui altura $x-b$. Provem les dues opcions:

$$ 2=\frac12\cdot x\cdot (x-a) \quad \Rightarrow \quad 4=x\cdot \left(x-\frac{40}x\right)=x^2-40 \quad \Rightarrow \quad x=\sqrt{44} $$

$$ 2=\frac12\cdot x\cdot (x-b) \quad \Rightarrow \quad 4=x\cdot \left(x-\frac{32}x\right)=x^2-32 \quad \Rightarrow \quad x=\sqrt{36}=6 $$

En cadascun dels dos casos, l'àrea del quart triangle serà:

$$ A=\frac12\cdot x\cdot (x-b) = \frac12 \sqrt{44}\cdot \left(\sqrt{44} - \frac{32}{\sqrt{44}}\right)=\frac12\cdot (44-32)=6 $$

$$ A=\frac12\cdot x\cdot (x-b) = \frac12 6\cdot \left(6 - \frac{40}6\right)=\frac12\cdot (36-40)=-2 \text{ (no pot ser!)} $$

Per tant, l'àrea del quart triangle és $6$ i la solució és la B.

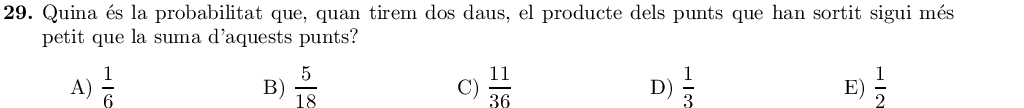
Al dau hi ha sis números: $1,2,3,4,5,6$. Adonem-nos que per tal que el producte de dos d'aquests números sigui més petit que la suma, un dels dos números ha de ser un $1$:

• Si un número és $1$, qualsevol que sigui l'altre, es complirà que $x+1 > 1\cdot x=x$.
• Si cap dels dos números és $1$, no es complirà mai. El cas que més s'apropa és quan surten dos $2$: $2+2 \ngtr 2\cdot 2$, i a partir d'aquí la diferència s'eixampla: $2+3 \ngtr 2\cdot 3$, $3+3 \ngtr 3\cdot 3$.

Així doncs, podem reformular l'enunciat com: quina és la probabilitat que surti algun número $1$ quan llancem els dos daus?

Per saber la probabilitat que surti algun $1$ hem de sumar la probabilitat que surti en el primer dau, més la probabilitat que surti en el segon, menys la probabilitat que surti en els dos (perquè és una possibilitat que hem comptat dos cops). El resultat és:

$$\frac16 + \frac16 - \frac16\cdot \frac16 = \frac{6 + 6 - 1}{36} = \frac{11}{36}$$

I la solució és la C.

Els divisors de $2016$ són els productes de totes les diferents combinacions dels seus factors primers. Aquests factors primers són:

$$2016=2^5\cdot 3^2\cdot 7$$

És a dir, per construir un divisor, podem posar el $2$ multiplicant un cop, dos cops... fins a $5$ cops, i de manera equivalent amb el $3$ i el $7$. En total hi ha:

$$\text{n. divisors} = (5+1)\cdot (2+1)\cdot (1+1) = 6\cdot 3\cdot 2 = 36$$

Dels $36$ divisors, la meitat tindran un $7$ com a factor, i l'altra meitat no en tindran cap. El producte de tots els divisors tindrà $\frac{36}{2}=18$ sets, i per tant l'única solució que pot ser correcta és $2016^{18}$ i la solució és la C.

Si comptem el nombre de vegades que apareixen el $2$ i el $3$ en el producte de tots els divisors, veurem també que apareixen $18\cdot 5$ i $18\cdot 2$ vegades respectivament.