La data consta de dos parts: el dia i el mes. Tots dos són números de com a molt dues xifres, i podem maximitzar la suma intentant que aquestes xifres siguen el més grans possibles. En el cas del mes, serà el $9$, i el dia el $29$.

El dia serà doncs el $29/9$, que suma $2+9+9=20$, i la solució és la E.

Ho podem fer pintant dos quadrats, de la següent manera:

I la solució és la A.

L'àrea d'un quadrat és el quadrat del seu costat:

$$A = \text{c}^2$$

Si l'àrea dels quadradets és $4$, el seu costat és $\text{c}=\sqrt{4}=2\text{ cm}$.

Com la línia gruixida està formada per $9$ costats, la seua longitud és: $9\cdot 2=18\text{ cm}$, i la solució és la B.

Anomenem $x, y$ els pesos dels dos sacs de parates. Sabem que si els pesem junts, pesen $80 \text{ kg}$:

$$x+y=80$$

i hem d'afegir $20\text{ kg}$ a un d'ells per igualar-lo a l'altre:

$$x=y+20$$

Per saber quant pesen hem de resoldre el sistema d'equacions. Aïllem la $x$ a la primera equació $(x=80-y)$, i substituïm a la segona:

$$80-y=y+20 \quad \Rightarrow \quad80-20=2y \quad \Rightarrow \quad $$ $$ y=30\quad \Rightarrow \quad x=50$$

El sac més pesat és $x$, que pesa $50\text{ kg}$, i la solució és la D.

En primer lloc, fixem-nos que a cada figura, els trossets que la composen (quadrats, rectangles o triangles) tenen la mateixa àrea, i per tant, sabrem la proporció ombrejada dividint el nombre de trossets ombrejats entre el total de trossets. Fem aquest càlcul, i les proporcions són:

$$ \text{A}=\frac{12}{20}, \quad \text{B}=\frac{9}{15}, \quad \text{C}=\frac{3}{5}, \quad \text{D}=\frac{3}{8}, \quad \text{E}=\frac{9}{15} $$

Si simplifiquem les fraccions traient els factors comuns, tenim:

$$ \text{A}=\frac{3}{5}, \quad \text{B}=\frac{3}{5}, \quad \text{C}=\frac{3}{5}, \quad \text{D}=\frac{3}{8}, \quad \text{E}=\frac{3}{5} $$

I la solució és la D, que és l'única amb una proporció diferent.

Si l'arbust té $9$ flors, tindrà $9$ branques amb una flor i quatre fulles; és a dir, de les $120$ fulles, $9\cdot 4=36$ estaran en branques amb una flor.

Queden $120-36=84$ fulles que estan en branques que tenen $7$ fulles cadascuna, és a dir, en $84:7=12$ branques.

En total, hi ha $9+12=21$ branques, i la solució és la B.

Solució 1

Ho podem solucionar ràpidament comptant. Fixem-nos que quan separem les tires $1\text{ cm}$, llavors la longitud total augmenta en $2\text{ cm}$, i que la longitud superposada disminueix en $2\text{ cm}$.

Si separem d'aquesta manera $3$ cops, la tira mesurarà $56\text{ cm}$ i la superfície superposada serà de $4\text{ cm}$: la A.

Solució 2

També podem esbrinar la mida de la tira plantejant-ho amb equacions.

Si anomenem $x$ la mida de les tires, quan les superposem, la longitud total és $2x$ menys el tros superposat. Sabem que en superposar $10\text{ cm}$ mesuren en total $50\text{ cm}$:

$$2x - 10 = 50 \quad\Rightarrow\quad x=30\text{ cm}$$

Sabem doncs que les tires són de $30\text{ cm}$. Si anomenem $y$ l'espai superposat, volem que:

$$2\cdot 30 -y = 56 \quad\Rightarrow\quad y=4\text{ cm}$$

I la solució és la A.

Si projectem cada costat del perímetre cap al quadrat que envolta la figura, veiem que el perímetre de la figura coincideix amb aquest quadrat exterior:

Com el costat del quadrat és $3$, el perímetre és $3\cdot 4=12$, i la solució és la B.

Anomenem $a, j, w, o$ les alçades d'Averell, Jack, William i Joe. Sabem que l'ordre és: $a > j > w > o$ i que les diferències són iguals. Anomenem $d$ aquesta diferència.

En Joe fa $160\text{ cm}$ és a dir, $o=160$. Sabem doncs, que:

$$o = 160, \quad w=160+d,\quad j=160+2d,\quad a=160+3d$$

Si la mitjana és 178, tenim que:

$$\frac{160 + (160+d) + (160+2d) + (160+3d)}{4}=178$$ $$\frac{160\cdot 4 + 6d}{4}=178 \quad\Rightarrow\quad 160 + \frac{3}{2}d = 178$$ $$\frac{3}{2}d = 18 \quad\Rightarrow\quad d=\frac{18\cdot 2}{3} \quad\Rightarrow\quad d=12$$

Aleshores, l'alçada de Jack és $j=160+2d=160+2\cdot 12=184$, és a dir, la A.

Si anomenem els triangles $A, B, C, D$ d'esquerra a dreta, podem dir que el triangle $B$ (el que conté el costat $x$), no pot tenir cap dels costats de sota de color vermell, ja que són costats compartits amb $A$ i $C$, que ja tenen un costat vermell (a la base). Aleshores, per tal que $B$ tingui un costat vermell, aquest ha de ser $x$.

Falta comprovar, que un cop decidit que $x=\text{vermell}$, es poden pintar la resta de costats. Efectivament, podem pintar els costats que falten (els costats verticals) d'esquerra a dreta de la següent forma: $\text{blau, verd, blau, verd, vermell}$, com podem veure a continuació:

Per tant, la solució és la C.

Justifiquem la solució amb la imatge següent:

En verd estan els quadrats on pot anar el cangur en $1$ moviment, i en rosa els quadrats des dels qual es pot arribar a la $A$. Com que no hi ha cap quadrat on coincideixin verd i rosa, no es pot anar a la $A$ en $2$ moviments.

Ara bé, sí que hi ha una casella verda i una rosa a un moviment de cangur, de manera que podem fer el camí en $3$ passos, tal com es mostra a la figura, i la solució és la D.

Si anomenem $a,b$ els costats d'un rectangle, la seua àrea i el seu perímetre són:

$$A=a\cdot b, \quad P=2a+2b$$

En el nostre cas, l'àrea és $12$, i volem esbrinar els diferents valors que poden prendre $a$ i $b$ que compleixin $a\cdot b=12$.

Amb l'ajuda de la factorització $12=2^2\cdot 3$, trobem els divisors: ${1, 2, 3, 4, 6}$. Vegem ara les diverses maneres d'expressar aquest producte, i el valor del perímetre que els correspon:

$$\begin{array}{lcl} A=12=1\cdot 12 &\Rightarrow& P=2\cdot 1+2\cdot 12=26 \\ A=12=2\cdot 6 &\Rightarrow& P=2\cdot 2+2\cdot 6=16 \\ A=12=3\cdot 4 &\Rightarrow& P=2\cdot 3+2\cdot 4=14 \end{array} $$

De les diferents opcions, l'únic valor que no és possibé és $24\text{ cm}$, la D.

Se'ns demana pel costat curt del rectangle gran, que és el mateix que el costat llarg dels rectangles petits.

Pel que fa als rectangles petits, observem que el costat llarg mesura el mateix que dos costats curts.

Llavors, la longitud de $10\text{ cm}$ equival a $2$ costats llargs de rectangle petit, i per tant la solució és $\frac{10}{2}=5\text{ cm}$, la E.

Per resoldre aquesta qüestió convé imaginar-se com es pleguen les figures, i si cal, ajudar-se amb un paper que es pot retallar. D'aquesta manera veiem que amb la C és impossible plegar una piràmide.

En total hi ha $9$ cases, per tant, la suma serà el nombre d'habitants de la primera casa, més les altres $4$ parelles de cases (però cada parella té $6$ habitants com a màxim). Per maximitzar la suma tota, voldríem posar $5$ persones a la primera casa. Vegem si ho podem fer:

$$ \begin{array}{|l|l|l|l|l|l|l|l|l|} 5 & 1 & 5 & 1 & 5 & 1 & 5 & 1 & 5 \end{array} $$

Efectivament, ho podem fer, i la solució és $5+4\cdot 6=29$ , la A.

Si sumem l'edat de la Mercè i el seu any de naixement, tindrem $2015$, pequè enguany ja ha complit anys. El mateix passarà amb la seva mare. Per tant, la solució serà $2015+2015=4030$ , la B.

Trobem les solucions sistemàticament, ja que no són massa:

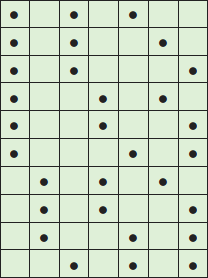
En total hi ha $10$ formes diferents de fer-ho, i la solució és la E.

Fixem-nos que cada allargador ocupa una endoll i n'afegeix tants com preses de corrent té. Per tant, els allargadors de $3$ afegeixen $3-1=2$ preses, i els de $5$ afegeixen $5-1=4$ preses. Com que d'inici tenim $1$ endoll, en total tindrem:

$$1+3\cdot 2+2\cdot 4=15$$

Tindrem $15$ preses disponibles: la B.

En el pitjor dels casos, primer traurà totes les peres verdes $(7)$ i totes les pomes grogues $(5)$. Finalment, haurà de traure $1$ peça més per repetir color.

En total, ha de traure $7+5+1=13$ , la A.

1. Si multipliquem $100$ per $2$ o $3$, podem tenir ${200, 300}$.
2. Si sumem $2$ o $1$, podem tenir ${201, 202, 301, 302}$.
3. En dividir per $4$ o $3$ ha de donar enter. Cap d'aquests números és divisible per $4$ i per $3$ només podem dividir el $201$: $\frac{201}{3}=67$.

La solució serà la C.

Recordem que la regla de divisibilitat pel $4$ és que el número format per les dues últimes xifres siga divisible per $4$; i que la norma de divisibilitat pel $3$ és que la suma de les xifres siga divisible per $3$.

Sumant dos números d'una xifra i un de dues xifres, mai podem obtenir un resultat tan gran com $200$, de manera que $ZZZ=111$.

Com que $X+X<20$, per tal d'arribar al $111$, $YY$ ha de ser $YY=99$.

Aleshores $X$ serà $X=\frac{111-99}{2}=6$.

Per tant, la solució és la C.

Solució 1

Si anomenem $x$ la quantitat que tenia inicialment, podem fer una taula amb tots els càlculs que s'expliquen a l'enunciat:

$$\begin{array}{cccc} \text{Pas}&\text{Diners que té}&\text{Diners que es gasta}&\text{Diners que li queden}\\ \\ 1 & x & \frac{x}{2}+1=\frac{x+2}{2} & x-\frac{x+2}{2}=\frac{x-2}{2} \\ \\ 2 & \frac{x-2}{2} & \frac{\frac{x-2}{2}}{2}+2=\frac{x+6}{4} & \frac{x-2}{2}-\frac{x+6}{4}=\frac{x-10}{4} \\ \\ 3 & \frac{x-10}{4} & \frac{\frac{x-10}{4}}{2}+3=\frac{x+14}{8} & \frac{x-10}{4}-\frac{x+14}{8}=\frac{x-34}{8} \end{array} $$

I sabem que al final s'ha quedat sense diners, és a dir:

$$\frac{x-34}{8}=0 \quad\Rightarrow\quad x=34$$

I la solució és la B.

Solució 2

Podem simplificar els càlculs adonant-nos que després de la primera operació, la Joana es queda amb la meitat dels diners menys $1$, després amb la meitat menys $2$ i per últim amb la meitat menys $3$. Com al final es queda amb $0$, podem expressar-ho tot amb una equació que anem resolent:

$$\frac{\frac{\frac{x}{2}-1}{2}-2}{2}-3=0 \quad\Rightarrow\quad \frac{\frac{x}{2}-1}{2}-2=6 \quad\Rightarrow$$ $$\frac{x}{2}-1=16 \quad\Rightarrow\quad x=34$$

Aquest problema l'hem d'imaginar espacialment, i ajudar-nos amb un paper si cal. Podem raonar per ordre:

1. Comprovem que traient el $3$ sí que es pot fer (descartem la A i la B).
2. Traient el $7$ també es pot fer: descartem la C.
3. Però traient el $4$ no es pot fer: descartem la E.

Per tant, la solució vàlida és la D.

Per saber les dues últimes xifres del resultat, només cal sumar les dues útimes xifres de cada terme de la suma. La suma queda:

$$9+\underbrace{99+\cdots+99}_{2014\ nombres}=9+99\cdot 2014=9+199.386=199.395$$

Les dues últimes xifres són $95$: la E.

Amb la condició que $A<B<C<D$, volem maximitzar $BD-AC$. Aquest resta és:

$$BD-AC=(10B+D)-(10A+C)=-10A+10B-C+D$$

La xifra que més resta és $A$, perquè està multiplicada per $-10$. Llavors triem la $A$ més petita possible: $A=1$.

La xifra que més suma és $B$, perquè està multiplicada per $10$. Volem triar $B$ el més gran possible, però no pot ser $9$ perquè $B<C<D$. Així que fem $B=7<C=8<D=9$.

La resta queda:

$$-10A+10B-C+D = -10 + 70 - 8 + 9 = 61$$

I la solució és la E.

Fixem-nos que els vèrtexs $C$ i $E$ estan oposats, de manera que entre els dos, sumen totes les cares del cub.

El mateix passa amb $D$ i $F$: com estan oposats, sumen totes les cares del cub. Llavors:

$$C+E=D+F$$

Volem saber el valor de $F$ i coneixem $C,D,E$, per tant:

$$14+24=16+F \quad \Rightarrow \quad F=22$$

I la solució és la B.

Anomenem $x$ el nombre de compartiments que té cada cotxe.

• Miquel viatja en el 3r cotxe i en el 18è compartiment. Aleshores, $18$ ha de ser major que el número de compartiments en els cotxes 1 i 2, i menor o igual al número de compartiments en el cotxe 3. És a dir, $2x<18\leq3x$ i si aïllem la $x$:

$$6\leq x<9$$

• Jana viatja en el 7è cotxe i el 50è compartiment, per tant, els primers $6$ cotxes tenen menys de $50$ compartiments, i els $7$ primers cotxes en tenen almenys $50$, és a dir: $6x<50\leq7x$. Aïllant la $x$:

$$7.1...\leq x<8.3...$$

Per l'última desigualtat i com $x$ és enter, $x=8$, i la solució és la D.

Centrant-nos en el vèrtex $C$, podem veure que $\widehat{QDP}=\widehat{QCD}$, i $\widehat{QBA}=\widehat{BCP}$, tal com es veu a la figura:

Aleshores, la suma dels tres angles és $\widehat{BCP}+\widehat{PCQ}+\widehat{QCD}=90^\circ$. I la solució és la C.

Entre els quatre punts hi ha tres distàncies $a, b, c$, que separen els quatre punts, tal com es mostra a la figura:

A més, hi haurà tres distàncies més: entre el primer i el tercer, $a+b$, entre el segon i el quart, $b+c$, i entre el primer i l'últim $a+b+c$.

La distància més gran, correspondrà amb la suma de totes tres:

$$a+b+c=14$$

I les dues següents, correspondran a les altres dues sumes indistintament:

$$a+b = 11 \quad\Rightarrow\quad 11 + c = 14 \quad\Rightarrow\quad c=3$$ $$b+c=12 \quad\Rightarrow\quad a + 12 = 14 \quad\Rightarrow\quad a=2$$ $$2+b=11 \quad\Rightarrow\quad b = 9$$

Així doncs, $k=9$, i la solució és la D.

En primer lloc, adonem-nos que només poden tenir dues cares diferents els cubs petits que es troben a les arestes dels cubs grans. D'aquests cubs petits hi ha:

• $8$ cubs petits que estan als vèrtexs del cub gran. Aquests tenen $3$ cares pintades.
• $2$ cubs petits que es troben enmig de cada aresta del cub gran, en total $2\cdot12=24$ cubs petits. Aquests tenen $2$ cares pintades.

L'enunciat ens diu que no hi ha cap cub petit amb les tres cares vermelles, és a dir, que no hi ha cap vèrtex on coincideixin tres cares vermelles. Això significa que tampoc hi ha cap vèrtex on coincideixin tres cares blaves. Per tant, els $8$ cubs petits dels vèrtexs tenen tots alguna cara vermella i alguna cara blava.

Pel que fa als $24$ cubs petits que hi ha a l'interior de les arestes, tindran els dos colors aquells que uneixin dues cares de diferent color.

Havent-hi $3$ cares vermelles i $3$ cares blaves, hi haurà $2$ arestes que uniran cares vermelles i $2$ arestes que uniran cares blaves. És a dir, $4$ de les $12$ arestes del cub gran uneixen cares del mateix color, i les $8$ arestes restants uneixen cares de diferent color.

Com cada aresta té $2$ cubs petits interiors, hi haurà $8\cdot2=16$ cubs petits situats enmig de les arestes i amb els dos colors.

En total, hi ha $8+16=24$ cubs petits amb ambdós colors, i la solució és la D.