Haskell és un llenguatge de programació funcional, molt diferent als llenguatges de programació als que estic més acostumat (C++, Python, JavaScript...). Fa un temps que sent parlar de Haskell; se sol destacar la seua elegància, els fonaments i inspiració matemàtica, i el fet que en ser un paradigma tan diferent a la programació imperativa ajuda a veure la programació des d'un altre punt de vista. Python, Java, C++... són tots llenguatges que estan incorporant conceptes de programació funcional a les seues versions més recents. Per tot això tenia ganes d'aprendre Haskell.

Logo de Haskell

Material

Vaig començar buscant llibres, tutorials, presentacions, etc. Per a mi, el millor llibre per iniciar-se és Learn You a Haskell for Great Good!. També és molt interessant i entretinguda aquesta presentació del professor de l'UJI Andrés Marzal (en dues hores i mitja comença presentant Haskell i acaba explicant funcionalitats bastant avançades), i que també inclou un bon pdf d'apunts. He fullejat el llibre Real World Haskell, que no em sembla el millor llibre per començar, però que té informació útil per desenvolupar projectes més grans.

Per practicar... el Jutge!

Una vegada convençut de les bondats de Haskell, volia posar-me a picar codi, però no tenia cap projecte en ment. Llavors vaig pensar en aprendre Haskell igual que vaig aprendre a programar en C++ fa anys: amb el Jutge.

El Jutge amb el clàssic semàfor: verd o roig segons si el teu programa és correcte o no.

El Jutge és una plataforma per aprendre a programar desenvolupada pels professors Jordi Petit i Salvador Roura de la UPC. Aquesta plataforma conté problemes que s'han de resoldre amb programes que cal enviar al mateix Jutge, el qual comprova automàticament si la seua execució és correcta. El Jutge s'usa a la UPC en assignatures de programació i algorísmia i el seu ús està obert a tot el públic, a més... conté 33 problemes d'un curs de programació en Haskell!

Així doncs, en les últimes setmanes he fet aquests 33 problemes :-). Ha sigut una experiència molt divertida, i un molt bon exercici per familiaritzar-me amb el llenguatge i l'entorn de programació.

Exemples de Haskell

A continuació faré un tast d'algunes funcionalitats de Haskell que són una mostra del potencial del llenguatge. Els conceptes estan explicats en profunditat a Learn You a Haskell for Great Good!, ací els presentaré i posaré alguns exemples de codi.

Treballant en Ubuntu, és recomanable instal·lar haskell-platform (sudo apt-get install haskell-platform) i usar l'intèrpret ghci. Per fer els programes, els guardem com en arxius prog.hs que defineixen les funcions que vulguem, i els podem carregar (i recarregar) amb ghci> :l prog per tal de provar les funcions que hem implementat.

Passem a veure aquestes funcionalitats tan interessants de Haskell...

Recursivitat

Haskell, com a llenguatge de programació funcional, no té bucles: ni while, ni for. Una manera d'implementar el que podríem fer amb bucles és mitjançant la recursivitat. Vegem un exemple amb la funció factorial, que és:

$$factorial(n) = n! = n\cdot (n-1)\cdots2\cdot 1$$

De manera recursiva, el podríem definir com:

$$\begin{cases} factorial(0) = 1 \\ factorial(n) = n\cdot factorial(n-1) \end{cases}$$

I en Haskell el podríem implementar així:

factorial :: Integer -> Integer
factorial 0 = 1
factorial n = n * factorial (n-1)

La primera línia és la signatura de la funció, que especifica el tipus del paràmetre i resultat. En el nostre cas, usem Integer, que són nombres enters de longitud arbitrària.

Llistes

Molts programes necessiten treballar amb llistes de valors, i Haskell ens ofereix moltes possibilitats per fer-ho de manera còmoda. Per exemple, vegem algunes maneres d'obtindre els nombres parells entre 0 i 20:

Prelude> [2,4..20]
[2,4,6,8,10,12,14,16,18,20]

Prelude> filter even [1..20]
[2,4,6,8,10,12,14,16,18,20]

Prelude> [x | x <- [1..20], even x]
[2,4,6,8,10,12,14,16,18,20]

Especialment curiosa és la última forma, anomanada llista per comprensió, que és molt similar a la notació matemàtica $\left\{x \; \vert \; \forall\, x \in {1,\ldots,20},\; esparell(x)\right\}$.

Usant recursivitat i llistes per comprensió, podem implementar l'algorisme d'ordenació quicksort. Donada una llista, el quicksort ordena els seus elements de la següent manera:

1. Tria el primer element com a pivot.
2. Sel·lecciona d'una banda tots els elements més petits que el pivot i de l'altra els mes grans, i els posa en dues llistes.
3. Ordena aquestes dues llistes usant el mateix quicksort.
4. El resultat és la llista dels petits ordenada, seguida del pivot, seguit de la llista dels grans ordenada.

Aquest algorisme es pot implementar amb Haskell d'una manera molt senzilla:

qsort :: [Int] -> [Int]
qsort [] = []
qsort (x:xs) =
    qsort [y | y <- xs, y <= x] ++ [x] ++ qsort [y | y <- xs, y > x]

Avaluació tardana

Haskell es basa completament en l'avaluació tardana, és a dir, que fa els càlculs tan tard com pot, i això és quan els necessita algú altre. Això permet, per exemple, tindre llistes infinites, perquè els valors de la llista només es calculen quan algú els demana. Per exemple:

Prelude> take 5 [1..]
[1,2,3,4,5]

Prelude> take 10 [1..]
[1,2,3,4,5,6,7,8,9,10]

Usant aquesta funcionalitat, podem implementar l'algorisme del garbell d'Eratòstenes que ens dóna la llista ordenada dels nombres primers.

El garbell d'Eratòstenes comença amb el número 2 (que és primer) i descarta tots els seus múltiples. Dels números que queden, agafa el més petit, que ha de ser primer perquè no és múltiple de cap altre nombre més petit que ell, i torna a descartar tots els seus múltiples.

Aquest procés dóna tots els primers més petits que un cert nombre donat: evidentment no podem descartar tots els nombres parells, perquè no acabaríem mai, el que podem fer és descartar tots els parells menors que 1000, per exemple. Haskell, però, com utilitza avaluació tardana, ens permet treballar amb llistes infinites i per tant tenir una implementació molt senzilla:

primers :: [Int]
primers = garbell [2..]
    where
        garbell (p:xs) = p : garbell [x | x <- xs, x `mod` p > 0]

Ho guardem a l'arxiu primers.hs i ho podem provar:

$ ghci
GHCi, version 7.6.3: http://www.haskell.org/ghc/  :? for help

Prelude> :l primers
[1 of 1] Compiling Main             ( primers.hs, interpreted )
Ok, modules loaded: Main.

*Main> take 5 primers
[2,3,5,7,11]

*Main> takeWhile (<50) primers
[2,3,5,7,11,13,17,19,23,29,31,37,41,43,47]

Funcions d'ordre superior

Les funcions d'ordre superior són funcions que prenen altres funcions com a paràmetres. Un exemple és la funció map, que pren una funció com a primer paràmetre i una llista com a segon paràmetre, i el que fa és aplicar la funció a cada element de la llista. Per exemple:

Prelude> map (*2) [1..10]
[2,4,6,8,10,12,14,16,18,20]

Prelude> map (^2) [1..10]
[1,4,9,16,25,36,49,64,81,100]

Per exemple, donada una llista d'enters i una llista d'exponents als quals volem elevar la primera llista, podríem fer:

Prelude> zipWith (^) [1..5] [1..5]
[1,4,27,256,3125]

Ací podeu trobar més exemples de funcions d'ordre superior i la seua utilitat.

Comprovació de patrons

Una altra funcionalitat molt interessant de Haskell és la comprovació de patrons (pattern matching en anglés). Per exemple, podem comprovar el patró (x:y:xs) sobre una llista, de manera que x i y representaran el primer i segon valor de la llista i xs la resta d'elements.

Vegem ara com podem usar el reconeixement de patrons per implementar el recorregut d'arbres binaris en diferents ordres. Primer recordem el preordre, inordre i postordre:

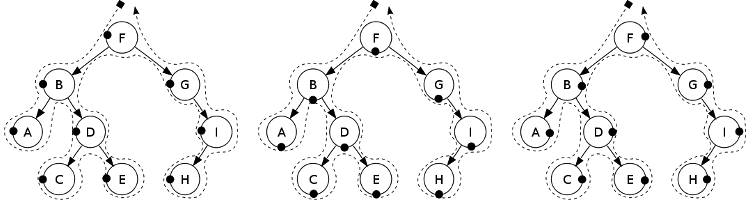Maneres de recórrer un arbre binari: preordre (esquerra: F,B,A,D,C,E,G,I,H), inordre (centre: A,B,C,D,E,F,G,H,I) i postordre (dreta: A,C,E,D,B,H,I,G,F). Els punts negres indiquen en quin moment del recorregut es tria cada node.

I açò ho podem implementar així:

data Tree a = Node a (Tree a) (Tree a) | Empty deriving (Show)

preOrdre :: Tree a -> [a]
preOrdre Empty = []
preOrdre (Node n t1 t2) = [n] ++ preOrdre t1 ++ preOrdre t2

postOrdre :: Tree a -> [a]
postOrdre Empty = []
postOrdre (Node n t1 t2) = postOrdre t1 ++ postOrdre t2 ++ [n]

inOrdre :: Tree a -> [a]
inOrdre Empty = []
inOrdre (Node n t1 t2) = inOrdre t1 ++ [n] ++ inOrdre t2

Les instruccions (Node n t1 t2) és on es realitza la comprovació de patrons.

Entrada / sortida

Vegem també un petit exemple d'entrada/sortida: un programa que llegeix el nom d'una persona i li diu Hola maca si el nom acaba en a i Hola maco altrament:

main :: IO()
main = do
    name <- getLine
    putStrLn $
        "Hola mac" ++
        (if elem (last name) "aA" then "a" else "o") ++ "!"

Producte de polinomis amb la Transformada Ràpida de Fourier

Per últim, vegem la implementació d'un algorisme més elaborat: la multiplicació de polinomis usant la Transformada Ràpida de Fourier. El producte de polinomis de grau $n$ té un cost d'$\mathcal{O}(n^2)$ si usem l'algorisme trivial: hem de multiplicar cada coeficient del primer polinomi per cada coeficient del segon polinomi, per després sumar com convinga, i això és quadràtic. Hi ha un algorisme molt més ràpid, que usa la Transformada Ràpida de Fourier, amb un cost d'$\mathcal{O}(n\log n)$.

Una molt bona explicació de com funciona aquest algorisme i de com implementar-lo la podeu trobar ací.

A continuació mostro la implementació, que amb a penes 12 línies de codi implementa la funció FFT, i amb 10 línies més implementa la multiplicació de polinomis.

import Data.Complex

fft :: [Complex Double] -> Complex Double -> [Complex Double]
fft [a] _ = [a]
fft a w = zipWith (+) f_even (zipWith (*) ws1 f_odd) ++
          zipWith (+) f_even (zipWith (*) ws2 f_odd)
    where
        -- Take even and odd coefficients of a(x)
        a_even = map fst $ filter (even . snd) (zip a [0..])
        a_odd  = map fst $ filter (odd  . snd) (zip a [0..])
        -- Compute FFT of a_even(x) and a_odd(x) recursively
        f_even = fft a_even (w^2)
        f_odd  = fft a_odd  (w^2)
        -- Compute 1st and 2nd half of unity roots (ws2 = - ws1)
        ws1 = take (length a `div` 2) (iterate (*w) 1)
        ws2 = map negate ws1

-- Multiplication of polynomials: c(x) = a(x) · b(x)
--     * a(x) and b(x) have degree n (power of 2), c(x) has degree 2n
--   Algorithm:
--     1. Compute f_a = fft(a), f_b = fft(b)  .. O(n·logn)
--     2. Compute product: f_c = f_a · f_c    .. O(n)
--     3. Interpolate c: c = fft^{-1}(f_c)    .. O(n·logn)
mult :: [Double] -> [Double] -> [Double]
mult [] _ = []
mult a b = map realPart c
    where
        n = length a
        w = exp (pi * (0 :+ 1) / fromIntegral n)
        f_a = fft (map (:+ 0) $ a ++ replicate n 0.0) w
        f_b = fft (map (:+ 0) $ b ++ replicate n 0.0) w
        f_c = zipWith (*) f_a f_b
        c = map (/ (fromIntegral $ 2*n)) $ fft f_c (1/w)

Per provar aquest programa, el guardem a l'arxiu fft.hs, obrim un intèrpret de Haskell ghci i carreguem el programa :l fft.hs. Podem provar de fer productes de polinomis amb mult [2,1] [3,-2]. Com quan treballem amb nombres de coma flotant (amb decimals) poden haver errors de precisió (per exemple enlloc de 2.0 el sistema pot guardar un 1.9999999999999996), definim la funció round2 que arrodoneix a dos decimals. A continuació teniu alguns exemples:

$ ghci
GHCi, version 7.6.3: http://www.haskell.org/ghc/  :? for help

Prelude> :l fft.hs
[1 of 1] Compiling Main             ( fft.hs, interpreted )
Ok, modules loaded: Main.

*Main> let round2 f = (fromInteger $ round $ f * 100) / 100

*Main> map round2 $ mult [2,1] [3,-2]
[6.0,-1.0,-2.0,0.0]

*Main> map round2 $ mult [2,1,0,0] [3,-2,0,0]
[6.0,-1.0,-2.0,0.0,0.0,0.0,0.0,0.0]

*Main> map round2 $ mult [3.5,-2,6,1] [3.5,-2,6,1]
[12.25,-14.0,46.0,-17.0,32.0,12.0,1.0,0.0]

*Main> map round2 $ mult [1,2,3,4,5,6,7,8] [0,0,0,0,1,0,0,0]
[0.0,0.0,0.0,0.0,1.0,2.0,3.0,4.0,5.0,6.0,7.0,8.0,0.0,0.0,0.0,0.0]